Đáp án B
Khi quay tam giác ABC quanh đường cao AH ta được hình nón có bán kính đường tròn đáy là R = BH= a 2 ,
đường sinh l = AB = a.
Vậy diện tích xung quanh là
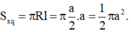
Đáp án B
Khi quay tam giác ABC quanh đường cao AH ta được hình nón có bán kính đường tròn đáy là R = BH= a 2 ,
đường sinh l = AB = a.
Vậy diện tích xung quanh là
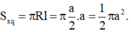
Cho tam giác đều ABC cạnh a quay xung quanh đường cao AH tạo nên một hình nón. Tính diện tích xung quanh S x q của hính nón đó.
![]()
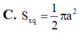
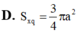
Cho hình nón có thiết diện qua trục là tam giác đều và có diện tích xung quanh bằng 8 π Tính chiều cao của hình nón này.
![]()
![]()
![]()
![]()
Cho tam giác ABC vuông cân tại B, cạnh AB = 2. Quay đường gấp khúc ACB quanh cạnh AB ta được hình nón. Tính diện tích xung quang của hình nón đó.
A . 8 π 2
B . 4 π 2
C . 4 π 3
D . 2 π 2
Cho tam giác ABC vuông tại B có AC=2a, BC=a khi quay tam giác ABC quay quanh cạnh góc vuông AB thì đường gấp khúc ABC tạo thành một hình nón tròn xoay có diện tích xung quanh bằng
![]()
![]()
![]()
![]()
Cho tam giác AOB vuông tại O, có O A B ^ = 30 0 và AB = a. Quay tam giác AOB quanh trục AO ta được một hình nón. Tính diện tích xung quanh S x q của hình nón đó.
A. S x q = πa 2 2
B. S x q = πa 2
C. S x q = πa 2 4
D. S x q = 2 πa 2
Cho hình nón ngoại tiếp hình chóp tứ giác đều có tất các các cạnh bằng a. Tính diện tích xung quanh S x q của hình nón đó.
![]()
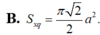
![]()
![]()
Cho hình nón đỉnh S và O là tâm đáy. Thiết diện qua trục của hình nón là một tam giác cân có đường cao h=3cm biết hai cạnh bên dài gấp đôi cạnh đáy. Tính diện tích xung quanh của hình nón đó.
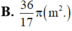
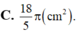

Cho tứ diện ABCD đều cạnh 3a. Tính diện tích xung quanh của hình nón có đỉnh là A, đường tròn đáy là đường tròn ngoại tiếp tam giác BCD.
A. 3 3 πa 2
B. 3 2 πa 2 2
C. 3 3 πa 2 2
D. 9 πa 2 4
Cho tam giác ABC nội tiếp trong đường tròn tâm O, bán kính R có B A C ^ = 75 0 , A C B ^ = 60 0 . Kẻ BH ⊥ AC. Quay quanh AC thì ∆ BHC tạo thành hình nón tròn xoay (N). Tính diện tích xung quanh của hình nón xoay (N) theo R.
A. 3 + 2 2 2 πR 2
B. 3 + 2 3 2 πR 2
C. 3 ( 1 + 2 ) 4 πR 2
D. 3 ( 1 + 3 ) 4 πR 2