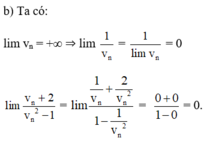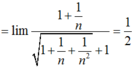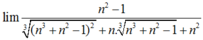Chủ đề / Chương

Bài học

Hãy tham gia nhóm Học sinh Hoc24OLM
Bạn chưa đăng nhập. Vui lòng đăng nhập để hỏi bài
Pham Trong Bach
Cho hai dãy số u n Biết lim u n     3 Tính giới hạn: l i m   3 u n - 1 u n  ...
Đọc tiếp
Lớp 11 Toán
Những câu hỏi liên quan
Quoc Tran Anh Le

Cho hai dãy số \(\left( {{u_n}} \right),\left( {{v_n}} \right)\) với \({u_n} = 3 + \frac{1}{n};{v_n} = 5 - \frac{2}{{{n^2}}}.\) Tính các giới hạn sau:

a) \(\lim {u_n},\lim {v_n}.\)

b) \(\lim \left( {{u_n} + {v_n}} \right),\lim \left( {{u_n} - {v_n}} \right),\lim \left( {{u_n}.{v_n}} \right),\lim \frac{{{u_n}}}{{{v_n}}}.\)

Xem chi tiết
Lớp 11 Toán Bài 1. Giới hạn của dãy số

Khách
 
Hà Quang Minh
Hà Quang Minh Giáo viên CTVVIP
22 tháng 9 2023 lúc 15:50

a) \(\begin{array}{l}\lim {u_n} = \lim \left( {3 + \frac{1}{n}} \right) = \lim 3 + \lim \frac{1}{n} = 3 + 0 = 3\\\lim {v_n} = \lim \left( {5 - \frac{2}{{{n^2}}}} \right) = \lim 5 - \lim \frac{2}{{{n^2}}} = 5 - 0 = 5\end{array}\)

b)

\(\begin{array}{l}\lim \left( {{u_n} + {v_n}} \right) = \lim {u_n} + \lim {v_n} = 3 + 5 = 8\\\lim \left( {{u_n} - {v_n}} \right) = \lim {u_n} - \lim {v_n} = 3 - 5 =  - 2\\\lim \left( {{u_n}.{v_n}} \right) = \lim {u_n}.\lim {v_n} = 3.5 = 15\\\lim \frac{{{u_n}}}{{{v_n}}} = \frac{{\lim {u_n}}}{{\lim {v_n}}} = \frac{3}{5}\end{array}\)

Bình luận (0)
Hán Bình Nguyên

a,CMR :dãy u(n)=\(\left(1+\dfrac{1}{n}\right)^n\)có giới hạ hữu hạn

b đặt lim(1+\(\dfrac{1}{n}\))^n =e .Tính các giưới hạn sau ; lim\(\left(\dfrac{n+1}{n-1}\right)^{n+2}\)và lim\(\left(\dfrac{n-2}{n+3}\right)^{n+1}\)

Xem chi tiết
Lớp 11 Toán Bài 1: Giới hạn của dãy số

Khách
 
Pham Trong Bach
Cho hai dãy số ( u n ) và ( v n ) . Biết l i m   u n     − ∞ và v n   ≤   u n  với mọi n. Có kết luận gì về giới hạn của dãy ( v n...
Đọc tiếp
Xem chi tiết
Lớp 11 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
3 tháng 2 2018 lúc 10:40

Vì l i m   u n   =   − ∞ nên l i m ( − u n )   =   + ∞ . Do đó ( − u n ) có thể lớn hơn một số dương lớn tuỳ ý, kể từ một số hạng nào đó trở đi. (1)

Mặt khác, vì v n   ≤   u n  với mọi n nên ( − v n )   ≥   ( − u n ) với mọi n. (2)

Từ (1) và (2) suy ra ( − v n ) có thể lớn hơn một số dương lớn tuỳ ý, kể từ một số hạng nào đó trở đi. Do đó, l i m ( − v n )   =   + ∞ hay   l i m   v n   =   − ∞

Bình luận (0)
Pham Trong Bach
Cho hai dãy số u n và v n . Biết | u n   –   2 |   ≤   v n  với mọi n và l i m   v n     0 . Có kết luận gì về giới hạn...
Đọc tiếp
Xem chi tiết
Lớp 11 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
24 tháng 4 2017 lúc 7:45

Lấy số dương ε bé tùy ý bất kì:

⇒ có một số n0 thỏa mãn: |vn| < ε kể từ n = n0.

⇒ |un – 2| < vn < |vn| < ε kể từ n = n0 trở đi

⇒ lim (un – 2) = 0

⇒ lim un = 2.

Bình luận (0)
Pham Trong Bach
Cho dãy số v n . Biết l i m   v n     +   ∞ . Tính các giới hạn:  l i m   v n   +   2...
Đọc tiếp
Xem chi tiết
Lớp 11 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
31 tháng 10 2019 lúc 4:03

Bình luận (0)
Pham Trong Bach
Tính giới hạn của dãy số Dlim n 2 + n + 1 - 2 n 3 + n 2 - 1...
Đọc tiếp
Xem chi tiết
Lớp 11 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
21 tháng 11 2019 lúc 2:08

Bình luận (0)
Pham Trong Bach
Tính giới hạn của dãy số D l i m ( n 2 + n + 1 - 2 n 3 + n 2 - 1 3...
Đọc tiếp
Xem chi tiết
Lớp 11 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
15 tháng 3 2017 lúc 10:05

Chọn C.

Ta có: 

Mà: 

Vậy .

Bình luận (0)
bao Le

Tính giới hạn của dãy:         A = lim\(\dfrac{\sqrt{1+2+3+...+n}}{n\left(n+999999\right)}\)

Xem chi tiết
Lớp 11 Toán Bài 1: Giới hạn của dãy số

Khách
 
Nguyễn Việt Lâm
Nguyễn Việt Lâm Giáo viên
5 tháng 12 2021 lúc 15:01

\(A=\lim\dfrac{\sqrt{\dfrac{n\left(n+1\right)}{2}}}{n\left(n+999999\right)}=\lim\dfrac{\sqrt{n^2+n}}{\sqrt{2}\left(n^2+999999n\right)}\)

\(=\lim\dfrac{\sqrt{\dfrac{1}{n^2}+\dfrac{1}{n^3}}}{\sqrt{2}\left(1+\dfrac{999999}{n}\right)}=\dfrac{0}{\sqrt{2}}=0\)

Bình luận (0)
CHANNANGAMI

tính giới hạn của dãy số C = lim \(\left(\sqrt{4n^2+n+1}-2n\right)\)

Xem chi tiết
Lớp 11 Toán Chương 4: GIỚI HẠN

Khách
 
...:v
...:v
8 tháng 2 2021 lúc 17:13

\(C=\lim\limits\dfrac{4n^2+n+1-4n^2}{\sqrt{4n^2+n+1}+2n}=\lim\limits\dfrac{\dfrac{n}{n}+\dfrac{1}{n}}{\sqrt{\dfrac{4n^2}{n^2}+\dfrac{n}{n^2}+\dfrac{1}{n^2}}+\dfrac{2n}{n}}=\dfrac{1}{2+2}=\dfrac{1}{4}\)

Bình luận (0)

Khoá học trên OLM (olm.vn)