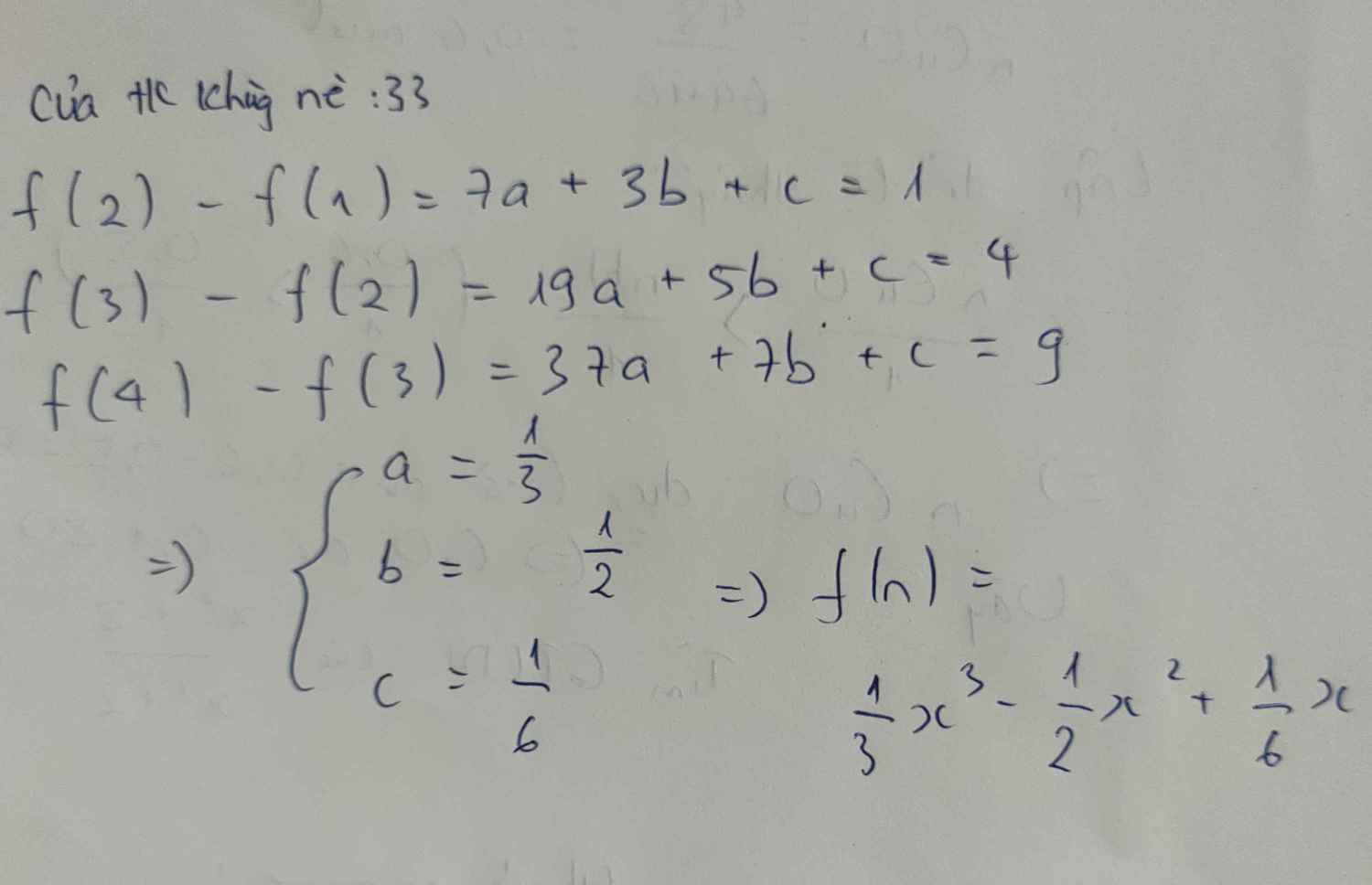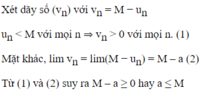Cho dãy số ( u n ) thoả mãn điều kiện: Với mọi n ∈ N ∗ thì 0 < u n < 1 v à u n + 1 < 1 - 1 4 u n Chứng minh dãy số đã cho là dãy giảm.

Những câu hỏi liên quan
Tìm các hằng số a, b, c sao cho đa thức f(x) =ax2 + bx + c thoả mãn điều kiện
f(n+1) – f(n) = n2 với mọi n = 1, 2, …
Không biết đề có vấn đề không nữa, tại vì không có cách nào để rút được c ra hết do f(n+1)-f(n) kiểu gì c cũng bị khử. Tuy nhiên nếu xét trường hợp với mọi c thì thay n=3 trở lên giải ngược lại không có nghiệm c nào thỏa mãn hết hehe nên là mình nghĩ đề sẽ kiểu "với n=1 hoặc n=2" . Theo mình nghĩ là vậy...
Giả sử n=1 ta có:
\(f\left(1+1\right)-f\left(1\right)=1\Leftrightarrow f\left(2\right)-f\left(1\right)=1\Leftrightarrow4a+2b+c-a-b-c=1\Leftrightarrow3a+b=1\) (1)
Giả sử n=2 ta có:
\(f\left(2+1\right)-f\left(2\right)=4\Leftrightarrow f\left(3\right)-f\left(2\right)=4\Leftrightarrow9a+3b+c-4a-2b-c=4\Leftrightarrow5a+b=4\) (2)
Từ (1) và (2) ta có: \(\left\{{}\begin{matrix}3a+b=1\\5a+b=4\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=\dfrac{3}{2}\\b=-\dfrac{7}{2}\end{matrix}\right.\)
\(\Rightarrow f\left(x\right)=\dfrac{3}{2}x^2-\dfrac{7}{2}x+c\) (với c là hằng số bất kì)
Đúng 0
Bình luận (0)
Cho dãy số ( u n ) thoả mãn u n > M với mọi n. Chứng minh rằng nếu l i m u n = a thì a ≤ M
Cho dãy số \(\left(u_n\right)\) thỏa mãn điều kiện : Với mọi \(n\in N^{\circledast}\) thì
\(0< u_n< 1\) và \(u_{n+1}< 1-\dfrac{1}{4u_n}\)
Chứng minh dãy số đã cho là dãy giảm
Cho dãy số (Un) thỏa mãn điều kiện: \(U_{n+1}-2U_n+U_{n-1}=1\) với \(n\ge1\). Hãy tính Un qua U0, U1 và n
Chỉ ra ba số tự nhiên m,n,p thoả mãn cho các điều kiện sau: m không chia hết cho p và n nhưng m + n chia hết cho b.
nếu:
n = 1
m = 1
b = 2
.có 1 ko chia hết cho 2
nhưng 1+1=2
Mà 2 ⋮ 2
➩n = 1
m = 1
b = 2
có nhiều lắm bạn ạ vd số nhỏ thôi nhé
Đúng 0
Bình luận (0)
Cho tam giác ABC a,tìm điểm M thoả mãn điều kiện vectơ MC vectơ CA vectơ MB vectơ 0 b,tìm N thoả mãn điều kiện vectơ NA vecto NB vectơ MC vectơ 0
Xem chi tiết
Cho tam giác ABC a,tìm điểm M thoả mãn điều kiện vectơ MC +vectơ CA +vectơ MB =vectơ 0 b,tìm N thoả mãn điều kiện vectơ NA- vecto NB+ vectơ MC= vectơ 0
Xem chi tiết
shsbdudjwosmgs
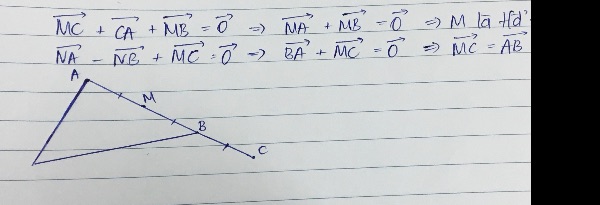
Cho phân số
A = \(\dfrac{13}{n-1}\)(n ∈ Z)
a, Số nguyên n phải thoả mãn điều kiện gì để phân số A tồn tại
b, Tìm phân só A khi n = 0; n = 5; n = 7
cho phân số A= 13/n-1 ( mọi n thuộc Z )
a) số nguyên n phải thỏ mãn điều kiện gì thì phân số A mới tồn tại
b ) tìm phân số A biết n=0 ; n=5 ; n=-5
c) với giá trị nào của n thì A là số nguyên?