Tập giá trị của hàm số y = sin 2x + 3 là:
A.[2;3]
B. [-2;3]
C. [2;4]
D. [0;1]
Tập giá trị của hàm số y = sin 2 x + 3 cos 2 x + 1 là đoạn [a;b]. Tính tổng T=a+b?
A.T=1
B.T=2
C.T=0
D.T=-1
Tập giá trị của hàm số y = sin 2x là
A. [-2;2]
B. [0;2]
C. [-1;1]
D. [0;1]
Tìm tập giá trị của các hàm số sau:
a) \(y = 2\cos \left( {2x - \frac{\pi }{3}} \right) - 1;\)
b) \(y = \sin x + \cos x\).
a) Tập xác định của hàm số là \(D = \mathbb{R}\)
Vì \( - 1 \le \cos \left( {2x - \frac{\pi }{3}} \right) \le 1 \Leftrightarrow - 2 \le 2{\rm{cos\;}}\left( {2x - \frac{\pi }{3}} \right) \le 2\;\; \Leftrightarrow - 3 \le 2\cos \left( {2x - \frac{\pi }{3}} \right) - 1 < 1\)
\( \Rightarrow \) Tập giá trị của hàm số \(y = 2\cos \left( {2x - \frac{\pi }{3}} \right) - 1\) là \(T = \left[ { - 3;1} \right]\).
b) Tập xác định của hàm số là \(D = \mathbb{R}\)
Vì \( - 1 \le \sin x \le 1,\;\; - 1 \le \cos \alpha \le 1\;\; \Leftrightarrow - 2 \le \sin x + \cos x \le 2\)
\( \Rightarrow \) Tập giá trị của hàm số \(y = \sin x + \cos x\) là \(T = \left[ { - 2;2} \right]\).
Tìm min, max và tập giá trị của hàm số:
1, y = 3sin(2x + \(\frac{\pi}{4}\) ) - 1
2, y = -5\(cos^2\) x + 3
3, y = \(\frac{5}{3\cos x+4}\)
4, y = \(\sin^2\)x - 4sinx + 8
1: Ta có: \(-1<=\sin\left(2x+\frac{\pi}{4}\right)\le1\)
=>\(-3\le3\cdot\sin\left(2x+\frac{\pi}{4}\right)\le3\)
=>\(-3-1\le3\cdot\sin\left(2x+\frac{\pi}{4}\right)-1\le3-1\)
=>-4<=y<=2
=>Tập giá trị là T=[-4;2]
\(y_{\min}=-4\) khi \(\sin\left(2x+\frac{\pi}{4}\right)=-1\)
=>\(2x+\frac{\pi}{4}=-\frac{\pi}{2}+k2\pi\)
=>\(2x=-\frac34\pi+k2\pi\)
=>\(x=-\frac38\pi+k\pi\)
2: \(0\le cos^2x\le1\)
=>\(0\ge-5\cdot cos^2x\ge-5\)
=>\(0+3\ge-5\cdot cos^2x+3\ge-5+3\)
=>3>=y>=-2
=>Tập giá trị là T=[-2;3]
\(y_{\max}=3\) khi \(cos^2x=1\)
=>\(\sin^2x=0\)
=>sin x=0
=>\(x=k\pi\)
\(y_{\min}=-2\) khi \(cos^2x=0\)
=>cosx=0
=>\(x=\frac{k\pi}{2}\)
3: \(-1\le cosx\le1\)
=>\(-3\le3\cdot cosx\le3\)
=>\(-3+4\le3\cdot cosx+4\le3+4\)
=>\(1\le3\cdot cosx+4\le7\)
=>\(\frac51\ge\frac{5}{3\cdot cosx+4}\ge\frac57\)
=>\(\frac57\le y\le5\)
=>Tập giá trị là \(T=\left\lbrack\frac57;5\right\rbrack\)
\(y_{\min}=\frac57\) khi cosx=1
=>\(x=k2\pi\)
\(y_{\max}=5\) khi cosx=-1
=>\(x=\pi+k2\pi\)
4: \(y=\sin^2x-4\cdot\sin x+8\)
\(=\sin^2x-4\cdot\sin x+4+4\)
\(=\left(\sin x-2\right)^2+4\)
Ta có: \(-1\le\sin x\le1\)
=>\(-1-2\le\sin x-2\le1-2\)
=>\(-3\le\sin x-2\le-1\)
=>\(1\le\left(\sin x-2\right)^2\le9\)
=>\(5\le\left(\sin x-2\right)^2+4\le13\)
=>5<=y<=13
=>Tập giá trị là T=[5;13]
\(y_{\min}=5\) khi sin x-2=-1
=>sin x=1
=>\(x=\frac{\pi}{2}+k2\pi\)
\(y_{\max}\) =13 khi sin x-2=-3
=>sin x=-1
=>\(x=-\frac{\pi}{2}+k2\pi\)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
a) \(y=f\left(x\right)=\dfrac{4}{\sqrt{5-2\cos^2x\sin^2x}}\)
b)\(y=f\left(x\right)=3\sin^2x+5\cos^2x-4\cos2x-2\)
c)\(y=f\left(x\right)=\sin^6x+\cos^6x+2\forall x\in\left[\dfrac{-\pi}{2};\dfrac{\pi}{2}\right]\)
Câu 1. Hàm số xác định \(\Leftrightarrow\cos x\ne0\Leftrightarrow x\ne\dfrac{\pi}{2}+k2\pi\)
Câu 2. có \(-1\le\sin3x\le1\Leftrightarrow2\le\sin3x+3\le4\)
tập giá trị của hàm số : [2;4]
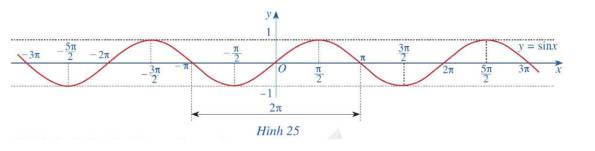
Quan sát đồ thị hàm số \(y = \sin x\) ở Hình 25.
a) Nêu tập giá trị của hàm số \(y = \sin x\)
b) Gốc tọa độ có là tâm đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số \(y = \sin x\)
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta có nhận được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\) hay không? Hàm số \(y = \sin x\)có tuần hoàn hay không/
d) Tìm khoảng đồng biến, nghịch biến của hàm số \(y = \sin x\)
a) Tập giá trị của hàm số\(y = \sin x\) là \(\left[ { - 1;1} \right]\)
b) Đồ thị hàm số \(y = \sin x\) nhận O là tâm đối xứng.
Như vậy hàm số \(y = \sin x\) là hàm số lẻ.
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta nhận được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\)
Như vậy, hàm số \(y = \sin x\) có tuần hoàn .
d) Hàm số \(y = \sin x\) đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\), nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\) với \(k \in Z\)
Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = sin x + 3
![]()
![]()
![]()
![]()
Tìm giá trị nhỏ nhất m của hàm số \(y=2\sin^2x+\sqrt{3}\sin2x\)
Lời giải:
$y=2\sin ^2x+\sqrt{3}\sin 2x=1-\cos 2x+\sqrt{3}\sin 2x$
$=1-(\cos 2x-\sqrt{3}\sin 2x)$
Áp dụng BĐT Bunhiacopxky:
$(\cos 2x-\sqrt{3}\sin 2x)^2\leq (\cos ^22x+\sin ^22x)(1+3)=4$
$\Rightarrow \cos 2x-\sqrt{3}\sin 2x\leq 2$
$\Rightarrow y=1-(\cos 2x-\sqrt{3}\sin 2x)\geq -1$
Vậy $y_{\min}=-1$. Giá trị này đạt tại $x=\frac{5\pi}{6}+2k\pi$ hoặc $x=\frac{-\pi}{6}+2k\pi$ với $k$ nguyên bất kỳ.