Gọi S là tập nghiệm của phương trình ln ( 3 e x - 2 ) = 2 x .Số tập con của S bằng
A. 0
B. 4
C. 1
D. 2
Có
ln 3 e x - 2 = 2 x ⇔ 3 e x - 2 = e 2 x . ⇔ e 2 x - 3 e x + 2 = 0 ⇔ [ e x = 1 e x = 2 ⇔ [ x = 0 x = ln 2
Vậy S có 2 phần tử nên có tất cả 2 2 = 4 tập con.
Chọn đáp án B.
Gọi E là tập nghiệm của phương trình \({x^2} - 2x - 3 = 0\).
G là tập nghiệm của phương trình \((x + 1)(2x - 3) = 0\)
Tìm \(P = E \cap G\).
Ta có:
\({x^2} - 2x - 3 = 0 \Leftrightarrow (x + 1)(x - 3) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 3\end{array} \right. \Rightarrow E = \{ - 1;3\} \)
Lại có: \((x + 1)(2x - 3) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = \frac{3}{2}\end{array} \right.\)
\( \Rightarrow G = \left\{ { - 1;\frac{3}{2}} \right\}\)
\( \Rightarrow P = E \cap G = \left\{ { - 1} \right\}\).
Xét phương trình \(x^2-2x-3=0\) có: \(a-b+c=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{c}{a}=3\end{matrix}\right.\Rightarrow E=\left\{-1;3\right\}.\)
Xét phương trình \(\left(x+1\right)\left(2x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+1=0\\2x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{3}{2}\end{matrix}\right.\Rightarrow G=\left\{-1;\dfrac{3}{2}\right\}.\)
\(\Rightarrow P=E\cap G=\left\{-1\right\}.\)
Gọi S là tập nghiệm của bất phương trình \(\dfrac{x^2+x+3}{x^2-4}\ge1\) . Khi đó S \(\cap\left(-2;2\right)\) là tập nghiệm nào
\(\dfrac{x^2+x+3}{x^2-4}\ge1\Leftrightarrow\dfrac{x^2+x+3}{x^2-4}-1\ge0\)
\(\Leftrightarrow\dfrac{x+7}{x^2-4}\ge0\Rightarrow\left[{}\begin{matrix}-7\le x< -2\\x>2\end{matrix}\right.\)
\(\Rightarrow S\cap\left(-2;2\right)=\varnothing\)
Cho hàm số f ( x ) = l n ( x 2 - 3 x ) . Tập nghiệm S của phương trình f'(x) = 0 là:
A. S = ∅
B. S = 3 2
C. S = {0;3}
D. S = - ∞ ; 0 ∪ 3 ; + ∞
Gọi S là tập nghiệm của phương trình 2 ( 2 x - 1 ) - 5 . 2 ( x - 1 ) + 3 = 0 . Tìm S.
A. S = {1; log23 }
B. S = {0; log 2 3 }
C. S = {1; log 3 2 }
D. S = {1}
Đáp án A
Phương pháp:
Đặt ẩn phụ, đưa về phương trình bậc hai một ẩn. Giải phương trình và suy ra ẩn t.
Cách giải:
Phương trình đã cho trở thành
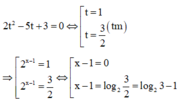
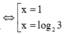
Gọi S là tập nghiệm của phương trình 2 l o g 2 ( 2 x - 2 ) + l o g 2 ( x - 3 ) 2 = 2 . Tổng các phần tử của S bằng:
A. 6
B. 4 + 2
C. 2 + 2
D. 8 + 2
Gọi S là tập nghiệm của phương trình 2 log 2 ( 2 x - 2 ) + log 2 ( x - 3 ) 2 = 2 trên ℝ . Tổng các phần tử của S là
A. 8 + 2
B. 4 + 2
C. 6 + 2
D. 8
Kí hiệu F (x) là một nguyên hàm của hàm số f ( x ) = 1 e x + 1 , biết F 0 = - ln 2 . Tìm tập nghiệm S của phương trình F ( x ) + ln ( e x + 1 ) = 3 .
A. S = - 3 ; 3
B. S = 3
C. S = ∅
D. S = - 3
Đáp án B
∫ 1 e x + 1 d x = ∫ d x - ∫ e x e x + 1 d x = x - ln ( e x + 1 ) + C
Vì F ( 0 ) = = - ln 2 ⇔ C = 0 ⇒ F ( x ) = x - ln e x + 1
Xét phương trình F ( x ) + ln ( e x + 1 ) = 3 ⇔ x = 3
Cho F(x) là một nguyên hàm của hàm số 1 e x + 1 , thỏa mãn F ( 0 ) = - ln 2 . Tìm tập nghiệm S của phương trình F ( x ) + l n ( e x + 1 ) = 3
A. S = 3
B. S = - 3
C. S = ∅
D. S = ± 3
