Biết ∫ 0 π 4 ( 1 + tan x ) 5 cos 2 x d x = a b ; trong đó a,b là 2 số nguyên dương và a/b là phân số tối giản. Mệnhđề nào dưới đây đúng?
A. a<b
B. ab = 1
C. a-10b = 1
D. a2 + b2 = 1
Phương trình tan( x - π/4) = 0 có nghiệm là:
A. x = π/4 + kπ, k ∈ Z.
B. x = 3π/4 + kπ, k ∈ Z.
C. x = kπ, k ∈ Z.
D. x = k2π, k ∈ Z.
Mấy bạnn giải chii tiết raa giúp mik với nhaa Câu 1: nghiệm dương nhỏ nhất của pt tan x=tan (6π/5) A. x=π/5 B. x=6π/5 C. x=6/5 D. x=6π Câu 2: tìm nghiệm thuộc đoạn [0;π] của pt cot 2x=cot(π/2-x) A. 2 B. 3 C.1 D.4 Câu 3: tìm tổng các nghiệm thuộc khoảng (-π/2;π/2) của pt 4sin²2x-1=0 A.0 B. π/6 C. π/3 D. π Câu 4: tìm tổng các nghiệm của pt cos(x+π/4)=1/2 trong khoảng (-π;π) A. π/2 B. -π/2 C. -3π/2 D. π/4
Biết sina = -4/5 với 3π/4 < a < π. Giá trị tan a là
A. 1/2 B. 2
C. -2 D. -1/2
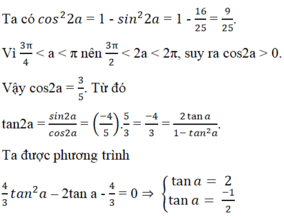
Vì 3π/4 < a < π nên tan a < 0. Vậy tan a = (-1)/2. Đáp án là D.
Nếu \(cot1,25.tan\left(4\text{ }Π+1,25\right)-sin\left(x+\frac{Π}{2}\right).cos\left(6Π-x\right)=0\) thì tanx bằng
\(cot1,25.tan\left(4\pi+1,25\right)-sin\left(x+\frac{\pi}{2}\right).cos\left(6\pi-x\right)=0\)
\(\Leftrightarrow cot1,25.tan1,25-cosx.cos\left(-x\right)=0\)
\(\Leftrightarrow1-cos^2x=0\)
\(\Leftrightarrow sin^2x=0\Rightarrow sinx=0\Rightarrow tanx=0\)
Giải pt: \( \tan ( 2x- \frac{ \pi }{ 3 } ) =- \frac{ 1 }{ 2 } \) với 0<x<π
ĐK: \(x\ne\dfrac{5\pi}{12}+\dfrac{k\pi}{2}\)
\(tan\left(2x-\dfrac{\pi}{3}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow2x-\dfrac{\pi}{3}=arctan\left(-\dfrac{1}{2}\right)+k\pi\)
\(\Leftrightarrow2x=\dfrac{\pi}{3}+arctan\left(-\dfrac{1}{2}\right)+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+\dfrac{1}{2}arctan\left(-\dfrac{1}{2}\right)+\dfrac{k\pi}{2}\in\left(0;\pi\right)\)
...
Giải phương trình sau: tanx + tan (x+π/4) = 1
Điều kiện:
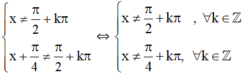
⇔ tan x.(1 - tanx) + tanx + 1 = 1 – tan x.
⇔ tan x - tan2x + 2.tan x = 0
⇔ tan2x - 3tanx = 0
⇔ tanx(tanx - 3) = 0
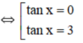
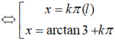
Vậy phương trình đã cho có tập nghiệm là:
{arctan 3+kπ; k ∈ Z }
Giá trị của biểu thức P=\(\left[tan\frac{17\text{Π }}{4}+tan\left(\frac{7\text{Π }}{2}-x\right)\right]^2+\left[cot\frac{13\text{Π }}{4}+cot\left(7\text{Π }-2\right)\right]^2\)
Có bao nhiêu giá trị nguyên của m ∈ ( - 15 ; 15 ) sao cho hàm số y = tan x - 10 tan x - m đồng biến trên khoảng 0 ; π / 4 ?
A. 20.
B. 9
C. 10.
D. 29.
Đáp án B
Đặt ![]() .
.
Với 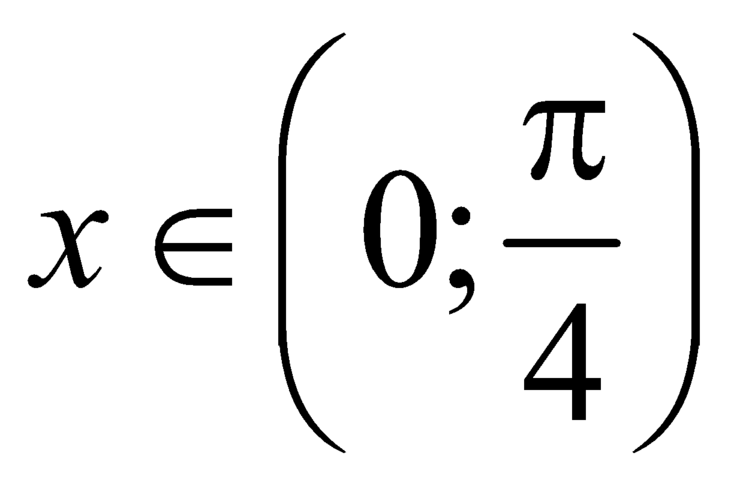 thì
thì ![]() , hàm số trở thành
, hàm số trở thành ![]() .
.
Đạo hàm 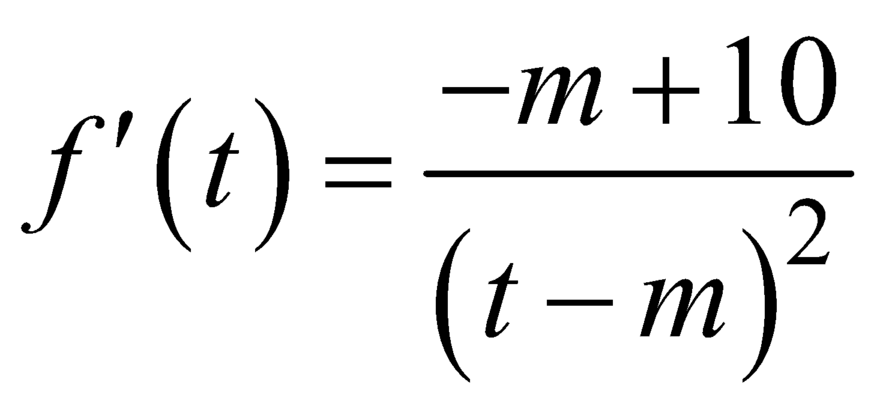 .
.
Hàm số đồng biến trên ![]() khi
khi
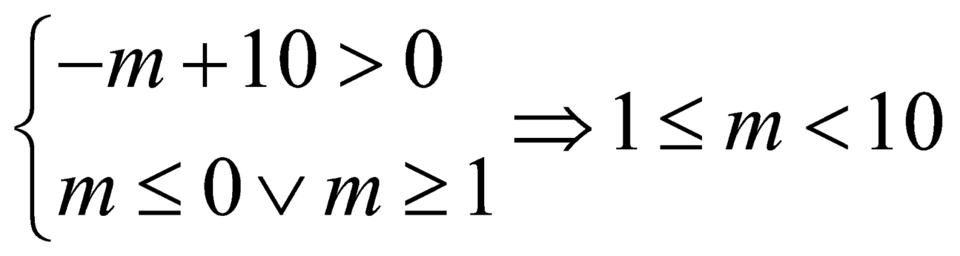 .
.
Vậy có 9 giá trị nguyên của m
giải phương trình sau: 2sinx-1=0 biết xϵ(-π/2: π)
\(2sinx-1=0\Leftrightarrow sinx=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
Do \(x\in\left(-\dfrac{\pi}{2};\pi\right)\Rightarrow x=\left\{\dfrac{\pi}{6};\dfrac{5\pi}{6}\right\}\)
Số nghiệm thuộc khoảng ( 0 ; π ) của phương trình. tan x + sin x + tan x - sin x = 3 tan x là
A. 0
B. 1
C. 2
D. 3