Giúp e giải theo đúg 4 bước đó ạ

Những câu hỏi liên quan
Giúp e các bước giải của bài này với ạ, e gấp lắm.E cảm ơn ạ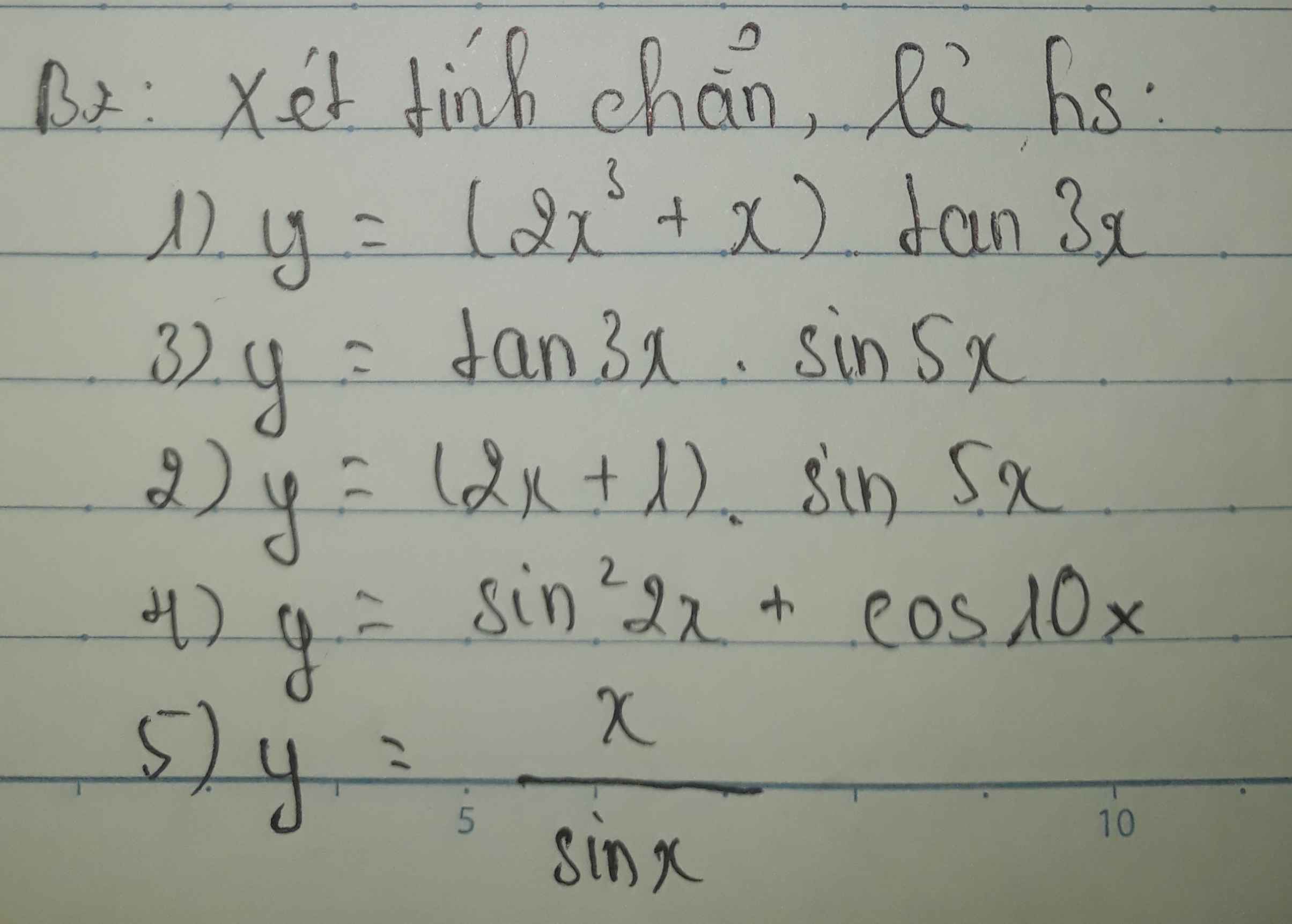
1.
\(D=R\backslash\left\{\dfrac{\pi}{6}+\dfrac{k\pi}{3}\right\}\) là miền đối xứng
\(f\left(-x\right)=\left(-x^3-x\right)tan\left(-3x\right)=\left(x^3+x\right)tan3x=f\left(x\right)\)
Hàm chẵn
2.
\(D=R\)
\(f\left(-x\right)=\left(-2x+1\right)sin\left(-5x\right)=\left(2x-1\right)sin5x\ne\pm f\left(x\right)\)
Hàm không chẵn không lẻ
3.
\(D=R\backslash\left\{\dfrac{\pi}{6}+\dfrac{k\pi}{3}\right\}\) là miền đối xứng
\(f\left(-x\right)=tan\left(-3x\right).sin\left(-5x\right)=-tan3x.\left(-sin5x\right)=tan3x.sin5x=f\left(x\right)\)
Hàm chẵn
4.
\(D=R\)
\(f\left(-x\right)=sin^2\left(-2x\right)+cos\left(-10x\right)=sin^22x+cos10x=f\left(x\right)\)
Hàm chẵn
5.
\(D=R\backslash\left\{k\pi\right\}\) là miền đối xứng
\(f\left(-x\right)=\dfrac{-x}{sin\left(-x\right)}=\dfrac{-x}{-sinx}=\dfrac{x}{sinx}=f\left(x\right)\)
Hàm chẵn
Đúng 1
Bình luận (0)
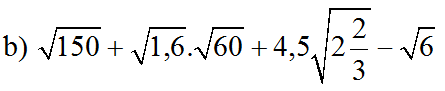
giải kỹ chi tiết từng bước giúp e với ạ!!!
e đang cần gấp lắm <3
b) Ta có: \(\sqrt{150}-\sqrt{1.6}\cdot\sqrt{60}+4.5\cdot\sqrt{2\dfrac{2}{3}}-\sqrt{6}\)
\(=5\sqrt{6}-4\sqrt{6}-\sqrt{6}+\dfrac{9}{2}\cdot\sqrt{\dfrac{8}{3}}\)
\(=\dfrac{9}{2}\cdot\dfrac{2\sqrt{2}}{\sqrt{3}}\)
\(=3\sqrt{6}\)
Đúng 1
Bình luận (1)
\(\sqrt{150}+\sqrt{1,6}.\sqrt{60}+4.5\sqrt{2\dfrac{2}{3}}-\sqrt{6}\\ =5\sqrt{6}+4\sqrt{6}+3\sqrt{6}-\sqrt{6}\\ =11\sqrt{6}\)
Đúng 0
Bình luận (0)
Mọi người giúp em câu n vs ạ giải từng bước giúp em, e c.ơn nhìu.
Bài 1: Cho A=(0,1,2,3,4,5,6,7,8,9).Có bao nhiêu số có 4 chữ số khác nhau thuộc (2000;9000).Giúp e các bước để giải bài này vs ạ
(2x -x2).(x2+2x-1)=0
Mng giải từng bước giúp e với ạ
=>x*(2-x)(x^2+2x-1)=0
=>x=0 hoặc 2-x=0 hoặc x^2+2x-1=0
=>x=0;x=2; \(x=-1\pm\sqrt{2}\)
Đúng 1
Bình luận (0)
Giúp e tìm tập xác định của các hs theo từng bước với ạ, do e ko giỏi phần này.E cảm ơn 
6.
Hàm số xác định khi \(\left\{{}\begin{matrix}2\sqrt{2}sinx-2\ne0\\sin3x\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}sinx\ne\dfrac{1}{\sqrt{2}}\\sin3x\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{4}+k2\pi\\x\ne\dfrac{3\pi}{4}+k2\pi\\x\ne\dfrac{k\pi}{3}\end{matrix}\right.\).
Đúng 1
Bình luận (0)
10.
Hàm số xác định khi \(\left\{{}\begin{matrix}sin\left(3x+\dfrac{\pi}{6}\right)\ne0\\cos2x\ne0\\sinx+1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}sin\left(3x+\dfrac{\pi}{6}\right)\ne0\\cos2x\ne0\\sinx+1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne-\dfrac{\pi}{18}+\dfrac{k\pi}{3}\\x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\x\ne-\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\).
Đúng 1
Bình luận (0)
5.
Hàm số xác định khi \(cos4x\ne0\Leftrightarrow x\ne\dfrac{\pi}{8}+\dfrac{k\pi}{4}\).
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải hệ phương trình(làm cụ thể các bước 1 tí giúp e với ạ)
Ta có:
\(x^2+y^2+\dfrac{1}{x^2}+\dfrac{1}{y^2}=4\)
\(\left(x^2-2+\dfrac{1}{x^2}\right)+\left(y^2-2+\dfrac{1}{y^2}\right)+4=4\)
\(\left(x-\dfrac{1}{x}\right)^2+\left(y-\dfrac{1}{y}\right)^2=0\)
Vì \(\left\{{}\begin{matrix}\left(x-\dfrac{1}{x}\right)^2\ge0\forall x\\\left(y-\dfrac{1}{y}\right)\ge0\forall y\end{matrix}\right.\)
Dấu "="⇔ \(\left\{{}\begin{matrix}x=\dfrac{1}{x}\\y=\dfrac{1}{y}\end{matrix}\right.\)
\(\Leftrightarrow x^2=y^2=1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=y=1\\x=y=-1\\x=1,y=-1\\x=-1,y=1\end{matrix}\right.\)
Thay vào phương trình 1
⇒ \(x=y=1\)
Đúng 3
Bình luận (0)
Mọi người giúp e các bước giải để tìm tập xác định các hs này với ạ, e cần gấp quá.E cảm ơn
1, Hàm số xác định
⇔ cos2x ≠ 4
Mà 0 ≤ cos2x ≤ 1 nên điều trên đúng ∀ x ∈ R
Tập xác định : D = R
2, Hàm số xác định ⇔ \(\left\{{}\begin{matrix}cos3x\ne0\\cosx\ne0\end{matrix}\right.\)
⇔ cos3x ≠ 0
⇔ x ≠ \(\pm\dfrac{\pi}{6}+k.\dfrac{\pi}{3}\) , k ∈ Z
Tập xác định : D = R \ { \(\pm\dfrac{\pi}{6}+k.\dfrac{\pi}{3}\) , k ∈ Z}
3, D = [- 2 ; 2]
4, D = [- 1 ; +\(\infty\)) \ {0 ; 4}
11, sin2x - cos2x ≠ 0
⇔ cos2x ≠ 0
Đúng 2
Bình luận (0)
Mng giúp em giải từng bước 4 câu này với ạ, em cảm ơn ạ

Câu 19:
\(=\dfrac{11x+x-18}{2x-3}=\dfrac{12x-18}{2x-3}=6\)
Câu 20:
\(=\dfrac{3x+5}{x\left(x-5\right)}+\dfrac{x-25}{5\left(x-5\right)}\)
\(=\dfrac{15x+25+x^2-25x}{5x\left(x-5\right)}=\dfrac{\left(x-5\right)^2}{5x\left(x-5\right)}=\dfrac{x-5}{5x}\)
Đúng 0
Bình luận (0)

















