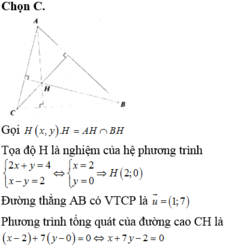
Cho tam giác ABC với H là trực tâm. Biết phương trình đường thẳng AB, BH và AH lần lượt là 4x + y – 12 = 0, 5x – 4y – 15 = 0 và 2x + 2y – 9 = 0. Hãy viết phương trình hai đường thẳng chứa hai cạnh còn lại và đường cao thứ ba.

Những câu hỏi liên quan
cho tam giác ABC có phương trình đường thẳng chứa cạnh AB là 5x - 3y + 2 = 0,và các đường cao kể từ A,B lần lượt có phương trình 4x - 3y + 1 = 0 và 7x + 2y - 22 = 0. viết phương trình các cạnh còn lại của tam giác ABC
Trong mặt phẳng với hệ trục tọa độ Oxy, hãy tính diện tích tam giác ABC biết rằng hai điểm H(5;5) và I(5;4) lần lượt là trực tâm và tâm đường tròn ngoại tiếp tam giác ABC và x+y-8=0 là phương trình đường thẳng chứa cạnh BC của tam giác.
Kéo dài đường cao AH lần lượt cắt BC và đường tròn ngoại tiếp tam giác ABC tại hai điển E và K, ta dễ dàng chứng minh được E là trung điểm HK
Đường cao \(AH\perp BC\) nên có phương trình \(x-y=0\), E là giao điểm của BC và AH \(\Rightarrow E\left(4;4\right)\) và H là trung điểm \(HK\Rightarrow K\left(3;3\right)\), suy ra bán kính đường tròn ngoại tiếp tam giác ABC là \(R=IK=\sqrt{5}\)
\(\Rightarrow\) phương trình đường tròn là \(\left(x-5\right)^2+\left(y-4\right)^2=5,\left(C\right)\)
Vậy hai điểm B, C là nghiệm của hệ hai phương trình đường thẳng BC và đường tròn (C) \(\Rightarrow B\left(3;5\right);C\left(6;2\right)\) và đỉnh A là nghiệm hệ của đường cao AH và đường tròn (C) \(\Rightarrow A\left(6;6\right)\)
Diện tích tam giác ABC là :
\(S_{ABC}=\frac{1}{2}d\left(A,BC\right).BC=\frac{1}{2}\frac{\left|6+6-8\right|}{\sqrt{2}}.3\sqrt{2}=6\)
Đúng 0
Bình luận (0)
Gọi H là trực tâm tam giác ABC; phương trình của các cạnh và đường cao tam giác là: AB: 7x – y+ 4 0 và BH: 2x+ y- 4 0; AH: x - y -2 0 Phương trình đường cao CH của tam giác ABC là: A. 7x- y+ 2 0 B. 7x+y-2 0 C. x+ 7y + 2 0 D. x+ 7y-2 0
Đọc tiếp
Gọi H là trực tâm tam giác ABC; phương trình của các cạnh và đường cao tam giác là:
AB: 7x – y+ 4= 0 và BH: 2x+ y- 4= 0; AH: x - y -2= 0
Phương trình đường cao CH của tam giác ABC là:
A. 7x- y+ 2= 0
B. 7x+y-2= 0
C. x+ 7y + 2= 0
D. x+ 7y-2= 0
Hai đường thẳng AH và BH cắt nhau tại H nên tọa đô của H là nghiệm hệ
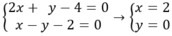
Vậy H( 2; 0)
Do CH vuông góc với AB mà AB: 7x – y + 4= 0 nên CH có
![]()
Suy ra; phương trình CH:
1(x-2) + 7( y-0) = 0
Hay x+ 7y -2= 0
Chọn D.
Đúng 0
Bình luận (0)
Gọi H là trực tâm của tam giác ABC. Phương trình các cạnh và đường cao của tam giác là AB: 7x-y+40; BH2x+y-40; AH: x-y-20. Phương trình đường cao CH của tam giác ABC là A. 7x-y0 B. x-7y-20 C. x+7y-20 D. 7x+y-20
Đọc tiếp
Gọi H là trực tâm của tam giác ABC. Phương trình các cạnh và đường cao của tam giác là AB: 7x-y+4=0; BH=2x+y-4=0; AH: x-y-2=0. Phương trình đường cao CH của tam giác ABC là
A. 7x-y=0
B. x-7y-2=0
C. x+7y-2=0
D. 7x+y-2=0
Lập phương trình đường thẳng chứa các cạnh của tam giác ABC biết A(1;-1), các đường trung trực của AB và BC lần lượt có phương trình là \(\Delta\): 2x - y + 1 = 0 và \(\Delta'\): x + 3y - 1 = 0
Đường thẳng AB nhận \(\overrightarrow{n}=\left(1;2\right)\) làm vecto pháp tuyến
AB đi qua A (1; -1) nên nó có phương trình là
x - 1 + 2 (y + 1) = 0 hay x + 2y + 1 = 0
Gọi M là trung điểm của AB ⇒ M ∈ Δ, tọa độ của M có dạng
M (t ; 2t + 1) với t là số thực và \(\overrightarrow{AM}=\left(t-1;2t+2\right)\)
⇒ AM ⊥ Δ
⇒ \(\overrightarrow{AM}.\overrightarrow{n}=0\)
⇒ t + 1 + 2. (2t + 2) = 0
⇒ t = -1
Vậy M (- 1; - 1)
M là trung điểm của AB => Tọa độ B
Làm tương tự như thế sẽ suy ra tọa độ C
Đúng 1
Bình luận (0)
Câu 60: Trong mặt phẳng Oxy, cho tam giác ABC có phương trình cạnh AB là x - y - 2 = 0 , phương trình đường thẳng chứa cạnh AC là x + 2y - 5 = 0 . Biết trọng tâm của tam giác là điểm G(3; 2) và phương trình đường thẳng chứa cạnh BC có dạng mx + ny + 7 = 0 . Giá trị của biểu thức T = m - n là ...
Tọa độ A là nghiệm: \(\left\{{}\begin{matrix}x-y-2=0\\x+2y-5=0\end{matrix}\right.\) \(\Rightarrow A\left(3;1\right)\)
\(\left\{{}\begin{matrix}x_A+x_B+x_C=3x_G\\y_A+y_B+y_C=3y_G\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_B+x_C=6\\y_B+y_C=5\end{matrix}\right.\) (1)
B thuộc AB nên: \(x_B-y_B=2\Rightarrow x_B=y_B+2\)
C thuộc AC nên: \(x_C+2y_C-5=0\Rightarrow x_C=-2y_C+5\)
Thế vào (1) \(\Rightarrow\left\{{}\begin{matrix}y_B+2-2y_C+5=6\\y_B+y_C=5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}y_B=3\Rightarrow x_B=5\\y_C=2\Rightarrow x_C=1\end{matrix}\right.\)
Phương trình BC: \(\dfrac{x-5}{1-5}=\dfrac{y-3}{2-3}\Leftrightarrow x-4y+7=0\)
Đúng 0
Bình luận (0)
Cho tam giác ABC biết trực tâm H(1;1) và phương trình cạnh AB: 5x -2y +6 0; phương trình cạnh AC: 4x + 7y -21 0 . Phương trình cạnh BC là: A. 4x- 2y +1 0 B. x-2y -14 0 C. x+ 2y -1 4 0 D. x- 2y + 14 0
Đọc tiếp
Cho tam giác ABC biết trực tâm H(1;1) và phương trình cạnh AB: 5x -2y +6 =0; phương trình cạnh AC: 4x + 7y -21= 0 . Phương trình cạnh BC là:
A. 4x- 2y +1= 0
B. x-2y -14= 0
C. x+ 2y -1 4= 0
D. x- 2y + 14 = 0
Đáp án B
Ta có AB và AC cắt nhau tại A nên tọa độ A là nghiệm hệ:
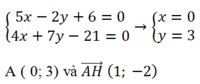
Ta có BH và AC vuông góc với nhau mà BH đi qua H (1;1) nên phương trình BH:
7(x-1) – 4( y-1) =0
Hay BH: 7x -4y – 3= 0
Có AB và BH cắt nhau tại B nên B( - 5; - 19/2 )
Phương trình BC nhận ![]() là VTPT và qua B
là VTPT và qua B
Suy r a (BC) : 1( x + 5) – 2( y+ 19/2) = 0 hay x- 2y -14 = 0
Đúng 0
Bình luận (0)
Cho tam giác ABC biết trực tâm H (1; 1) và phương trình cạnh AB: 5x- 2y+ 6=0, phương trình cạnh AC: 4x+ 7y -21= 0. Phương trình cạnh BC là:
A. 4x- 2y+1= 0
B. x- 2y + 14= 0
C.x- 2y+ 8 = 0
D. x- 2y- 14= 0
Đáp án :D
+Ta có hai đường thẳng AB và AC cắt nhau tại A nên tọa độ điểm A là nghiệm hệ phương trình:
5 x - 2 y + 6 = 0 4 x + 7 y - 21 = 0 → A ( 0 ; 3 ) v à A H → ( 1 ; - 2 )
+Ta có BH vuông góc với AC nên đường thẳng BH qua H(1;1) và nhận vecto u → ( 4 ; 7 ) làm VTCP và u → ( 7 ; - 4 ) làm VTPT
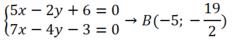
Suy ra phương trình đường thẳng BH là:
7( x-1) – 4( y-1) =0
=> 7x- 4y -3= 0
+ ta có AB và BH cắt nhau tại B nên tọa độ điểm B là nghiệm hệ phương trình:
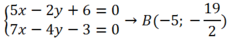
+Phương trình BC nhận A H → ( 1 ; - 2 ) là VTPT và qua B ( - 5 ; - 19 2 )
Suy ra phương trình (BC) :
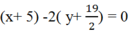
Hay x-2y-14= 0 .
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Biết đường thẳng chứa cạnh đáy BC có phương trình \(x-2y+3=0\), phương trình đường thẳng chứa cạnh bên AB là \(4x-y+5=0\) và điểm P(1;2;5;6) nằm trên đường thẳng AC. Viết phương trình của đường thẳng chứa cạnh AC của tam giam giác
Điểm P có tọa độ \(\left(\frac{5}{6};\frac{28}{5}\right)\). Đặt \(\widehat{ABC}=\alpha\). Do tam giác ABC cân tại A nên \(\alpha\in\left(0;\frac{\pi}{2}\right)\) do đó \(\alpha=\left(\widehat{AB,BC}\right)=\left(\widehat{BC,CA}\right)\)
và \(\cos\alpha=\frac{\left|4.1+\left(-1\right).\left(-2\right)\right|}{\sqrt{4^2+\left(-1\right)^2}.\sqrt{1^2+\left(-2\right)^2}}=\frac{6}{\sqrt{5.17}}\)
Do đó bài toán trở thành viết phương trình đường thẳng đi qua \(P\left(\frac{6}{5};\frac{28}{7}\right)\) không song song với AB, tạo với BC góc \(\alpha\) mà \(\cos\alpha=\frac{6}{\sqrt{5.17}}\) (1)
Đường thẳng AC cần tìm có vecto pháp tuyến \(\overrightarrow{n}=\left(a;b\right)\) với \(a^2+b^2\ne0\) và \(a\ne-4b\) (do AC không cùng phương với AB). Từ đó và (1) suy ra :
\(\frac{6}{\sqrt{5.17}}=\frac{\left|a-2b\right|}{\sqrt{5}.\sqrt{a^2+b^2}}\Leftrightarrow6\sqrt{a^2+b^2}=\sqrt{17}.\left|a-2b\right|\)
\(\Leftrightarrow19a^2+68ab-32b^2=0\)
\(\Leftrightarrow\left(a+4b\right)\left(19a-8b\right)=0\)
\(\Leftrightarrow19a=8b\) (do \(a\ne-4b\) (2)
Từ (2) và do \(a^2+b^2\ne0\), chọn a=40, b=95 được phương trình đường thẳng AC cần tìm là \(40\left(x-\frac{6}{5}\right)+95\left(y-\frac{28}{5}\right)=0\) hay \(8x+19y-116=0\)
Đúng 0
Bình luận (0)