Các câu hỏi tương tự
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có M(2;0) là trung điểm của cạnh AB. Đường trung tuyến và đường cao qua đỉnh A lần lượt có phương trình là 7x-2y-3=0 và 6x-y-4=0. Phương trình đường thẳng AC là:
A.3x-4y-5=0
B.3x+4y+5=0
C.3x-4y+5=0
D.3x+4y-5=0
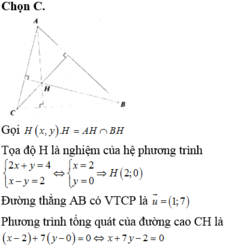
Cho tam giác ABC. Biết ba cạnh của tam giác AB,AC,BC. có phương trình lần lượt là 3x+4y-2=0, y-2=0, x-2=0. Phương trình tổng quát đường phân giác trong AD của tam giác ABC
A. 3x-y+8=0
B. x+2y=0
C. x+3y-8=0
D. x+3y-4=0
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có tâm đường tròn ngoại tiếp là điểm J(4;0) và phương trình hai đường thẳng lần lượt chứa đường cao và đường trung tuyến từ đỉnh A của tam giác ABC là
d
1
:
x
+
y
–
2
0
và
d
2
:
x
+
...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có tâm đường tròn ngoại tiếp là điểm J(4;0) và phương trình hai đường thẳng lần lượt chứa đường cao và đường trung tuyến từ đỉnh A của tam giác ABC là d 1 : x + y – 2 = 0 và d 2 : x + 2 y - 3 = 0 . Tìm tọa độ điểm C, biết B có tung độ dương.
A. C(3;-3).
B. C(7;1).
C. C(1;1).
D. C(-3;-9).
cho tam ABC có trung điểm cạnh AB là M(-1;1) gọi N là trung điểm AC. biết trung tuyến BN có phương trình: x-6y-3=0 đường ca Ah có phương trình: 4x-y-1=0 hãy viết phương trình các cạnh tam giác
cho tam giác ABC nhọn có trực tâm H.đường thẳng qua BC có phương trình y+1=0.gọi A1,B1 là các điểm đối xứng của H qua các trung điểm của các cạnh BC,AC.biết A1(0,-3),B1(2,2),viết phương trình cạnh AB
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(2;1), đường cao BH có phương trình x - 3 y - 7 = 0 và trung tuyến CM có phương trình x + y + 1 = 0 . Tìm tọa độ đỉnh C
A. (-1;0)
B. (4;-5)
C. (1;-2)
D. (1;4)
a) Cho tam giác ABC có C(-1;-2) đường trung tuyến kẻ từ A và đường cao kẻ từ B lần lượt có phương trình 5x+y-9=0 và x+3y-5=0. Tìm tọa độ A, B
b) Cho đường thẳng a: x-2y-3=0 và b: x+y+1=0. Tìm tọa độ điểm M trên a sao cho khoảng cách từ M đến b là 1/ căn 2
Trong hệ tọa độ Oxy cho tam giác ABC có phương trình đường thẳng BC: x+7y-13=0. Các chân đường cao kẻ từ B, C lần lượt là E(2;5), F(0;4). Biết tọa độ đỉnh A là A(a;b). Khi đó
A. a-b=5
B. 2a+b=6
C. a+2b=6
D. b-a=5
trong mặt phảng hệ tạo độ Oxy cho tam giác ABC có đỉnh A(1;2), đường trung tuyến BM và đường phân giác trong CD có phương trình tương ứng là 2x+y=0; x+y-1=0. Hãy viết PT đường thẳng BC.