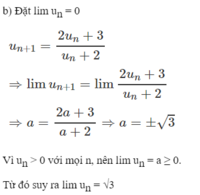Cho biết dãy số ( u n ) có giới hạn hữu hạn, còn dãy số ( v n ) không có giới hạn hữu hạn. Dãy số ( u n + v n ) có thể có giới hạn hữu hạn không?

Những câu hỏi liên quan
Cho biết dãy số \(\left(u_n\right)\) có giới hạn hữu hạn, còn dãy số \(\left(v_n\right)\) không có giới hạn hữu hạn. Dãy số \(\left(u_n+v_n\right)\) có thể có giới hạn không ?
Cho dãy số
(
u
n
)
xác định bởi
u
1
1
u
n
+
1...
Đọc tiếp
Cho dãy số ( u n ) xác định bởi u 1 = 1 u n + 1 = 2 u n + 3 u n + 2 v ớ i n ≥ 1
a) Chứng minh rằng u n > 0 với mọi n.
b) Biết ( u n ) có giới hạn hữu hạn. Tìm giới hạn đó.
cho dãy số \(\left(u_n\right)\) được xác định như sau: \(\hept{\begin{cases}u_1=u_2=1\\u_{n+1}=\sqrt{u_n}+\sqrt{u_{n-1}},\end{cases}\left(n\ge2,n\in N\right)}\)
Chứng minh dãy \(\left(u_n\right)\)có giới hạn hữu hạn. Tính giới hạn đó.
Cho dãy số
(
u
n
)
xácđịnh bởi công thức truy hồi
u
1
2
u
n
+...
Đọc tiếp
Cho dãy số ( u n ) xácđịnh bởi công thức truy hồi u 1 = 2 u n + 1 = u n + 1 2 v ớ i n ≥ 1
Chứng minh rằng có giới hạn hữu hạn khi Tìm giới hạn đó.
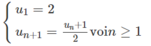
Ta có
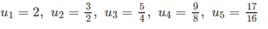
Dự đoán

Chứng minh dự đoán trên bằng quy nạp (bạn đọc tự chứng minh).
Từ đó
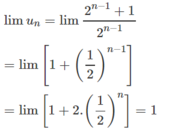
Đúng 0
Bình luận (0)
Cho dãy số thực (un) xác định bởi : \(\left\{{}\begin{matrix}u_1=\dfrac{3}{2}\\u_n=\sqrt{3u_{n-1}-2},\forall n\ge2\end{matrix}\right.\)
Chứng minh dãy số (un) có giới hạn hữu hạn khi \(n\rightarrow\infty\)
Ta sẽ chứng minh dãy bị chặn trên bởi 2
Thật vậy, với \(n=1;2\) thỏa mãn
Giả sử điều đó cũng đúng với \(n=k\) , tức \(u_k< 2\)
Ta cần chứng minh \(u_{k+1}< 2\)
Ta có: \(u_{k+1}=\sqrt{3u_k-2}< \sqrt{3.2-2}=2\) (đpcm)
Tương tự, ta cũng quy nạp được dễ dàng \(u_n>1\)
Mặt khác: \(u_n-u_{n-1}=\sqrt{3u_{n-1}-2}-u_{n-1}=\dfrac{3u_{n-1}-2-u_{n-1}^2}{\sqrt{3u_{n-1}-2}+u_{n-1}}\)
\(=\dfrac{\left(2-u_{n-1}\right)\left(u_{n-1}-1\right)}{\sqrt{3u_{n-1}-2}+u_{n-1}}>0\)
\(\Rightarrow u_n>u_{n-1}\Rightarrow\) dãy tăng
Dãy tăng và bị chặn trên nên có giới hạn hữu hạn.
Gọi giới hạn đó là k thì:
\(k=\sqrt{3k-2}\Leftrightarrow k=2\)
Đúng 1
Bình luận (0)
Cho dãy số (\(u_n\)) xác định bởi: \(\left\{{}\begin{matrix}0< u_n< 1\\u_n\left(1-u_{n+1}\right)>\dfrac{1}{4},\forall n\ge1\end{matrix}\right.\)
Chứng minh dãy số (\(u_n\)) có giới hạn hữu hạn khi \(n\rightarrow\infty\)
\(u_n-u_{n+1}=u_n+\left(1-u_{n+1}\right)-1\ge2\sqrt{u_n\left(1-u_{n+1}\right)}-1>0\)
\(\Rightarrow u_n>u_{n+1}\Rightarrow\) dãy giảm
Dãy giảm và bị chặn dưới bởi 0 nên có giới hạn hữu hạn.
Gọi giới hạn đó là k
\(\Rightarrow k\left(1-k\right)\ge\dfrac{1}{4}\Rightarrow\left(2k-1\right)^2\le0\Rightarrow k=\dfrac{1}{2}\)
Vậy \(\lim\left(u_n\right)=\dfrac{1}{2}\)
Đúng 3
Bình luận (0)
Biết rằng dãy số
(
u
n
)
có giới hạn là 0. Giải thích vì sao dãy số
(
v
n
)
với
v
n
|
u
n
|
cũng có giới hạn là 0. Chiều ngược lại có đúng không?
Đọc tiếp
Biết rằng dãy số ( u n ) có giới hạn là 0. Giải thích vì sao dãy số ( v n ) với v n = | u n | cũng có giới hạn là 0. Chiều ngược lại có đúng không?
Vì ( u n ) có giới hạn là 0 nên | u n | có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi.
Mặt khác, | v n | = | | u n | | = | u n | . Do đó, | v n | cũng có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi. Vậy ( v n ) có giới hạn là 0.
Đúng 0
Bình luận (0)
Cho dãy số (Un) được xác định như sau: \(u_1=2023\), \(u_{n-1}=n^2.\left(u_{n-1}-u_n\right)\), với mọi n thuộc N*, \(n\ge2\). Chứng minh rằng dãy số (Un) có giới hạn và tìm giới hạn đó
Cho dãy số (Un) được xác định như sau \(u_1=2023\), \(u_{n-1}=n^2.\left(u_{n-1}-u_n\right)\), với mọi n thuộc N*, \(n\ge2\) . Chứng minh rằng dãy số (Un) có giới hạn và tìm giới hạn đó