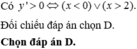Xét tính liên tục của các hàm số sau: f ( x ) = x + 5 t ạ i x = 4

Những câu hỏi liên quan
Xét tính liên tục của các hàm số sau trên TXĐ của chúng
f(x)= {x2-3x +4 khi x<2
{ 5 khi x=2
{2x +1 khi x>2
`TXĐ: R`
`@` Nếu `x > 2` thì: `f(x)=2x+1`
H/s xác định trên `(2;+oo)`
`=>` H/s liên tục trên `(2;+oo)`
`@` Nếu `x < 2` thì: `f(x)=x^2-3x+4`
H/s xác định trên `(-oo;2)`
`=>` H/s liên tục trên `(-oo;2)`
`@` Nếu `x=2` thì: `f(x)=5`
`lim_{x->2^[-]} (x^2-3x+4)=2`
`lim_{x->2^[+]} (2x+1)=5`
Vì `lim_{x->2^[-]} f(x) ne lim_{x->2^[+]} f(x) =>\cancel{exists} lim_{x->2} f(x)`
`=>` H/s gián đoạn tại `x=2`
KL: H/s liên tục trên `(-oo;2)` và `(2;+oo)`
H/s gián đoạn tại `x=2`
Đúng 1
Bình luận (0)
Xét tính liên tục của các hàm số sau trên tập xác định của chúng
f
(
x
)
x
2
-
2
x
-...
Đọc tiếp
Xét tính liên tục của các hàm số sau trên tập xác định của chúng f ( x ) = x 2 - 2 x - 2 n ế u x ≠ 2 2 2 n ế u x = 2
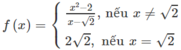
Tập xác định của hàm số là D = R
- Nếu x ≠ √2 thì 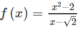
Đây là hàm phân thức hữu tỉ nên liên tục trên các khoảng (-∞; √2) và (√2; +∞)
- Tại x = √2:
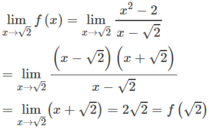
Vậy hàm số liên tục tại x = √2
Kết luận : y = f(x) liên tục trên R
Đúng 0
Bình luận (0)
Xét tính liên tục của hàm số sau tại điểm
x
0
2
f
(
x
)
2
x
2
-
3
x
-
2
k
h
i
...
Đọc tiếp
Xét tính liên tục của hàm số sau tại điểm x 0 = 2
f ( x ) = 2 x 2 - 3 x - 2 k h i x ≠ 2 3 2 k h i x = 2
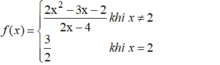
- Tập xác định D = R.
- Ta có: f(2) = 3/2.
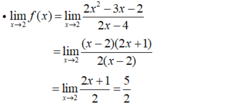
- Vì 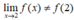 nên hàm số không liên tục tại x = 2.
nên hàm số không liên tục tại x = 2.
Đúng 0
Bình luận (0)
xét tính liên tục của hàm số sau tại x = 5
\(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^2-8x+15}{x-5}\\2x-1\end{matrix}\right.\) khi \(x\ne5\); khi \(x=5\)
\(\lim\limits_{x\rightarrow5}f\left(x\right)=\lim\limits_{x\rightarrow5}\dfrac{x^2-8x+15}{x-5}\)
\(=\lim\limits_{x\rightarrow5}\dfrac{\left(x-3\right)\left(x-5\right)}{x-5}=\lim\limits_{x\rightarrow5}x-3=5-3=2\)
f(5)=2*5-1=9
=>\(f\left(5\right)\ne\lim\limits_{x\rightarrow5}f\left(x\right)\)
=>Hàm số gián đoạn tại x=5
Đúng 0
Bình luận (0)
xét tính liên tục của hàm số sau tại \(x_0\) = 5
\(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{\sqrt{2x-9}-1}{5-x}\\3\end{matrix}\right.\) khi \(x\ne5\); khi \(x=5\)
\(\lim\limits_{x\rightarrow5}f\left(x\right)=\lim\limits_{x\rightarrow5}\dfrac{\sqrt{2x-9}-1}{5-x}\)
\(=\lim\limits_{x\rightarrow5}\dfrac{2x-9-1}{\sqrt{2x-9}+1}\cdot\dfrac{1}{5-x}\)
\(=\lim\limits_{x\rightarrow5}\dfrac{2\left(x-5\right)}{-\left(x-5\right)\left(\sqrt{2x-9}+1\right)}\)
\(=\lim\limits_{x\rightarrow5}\dfrac{-2}{\sqrt{2x-9+1}}=\dfrac{-2}{\sqrt{10-9}+1}=-\dfrac{2}{2}=-1\)
f(5)=3
=>\(\lim\limits_{x\rightarrow5}f\left(x\right)< >f\left(5\right)\)
=>Hàm số bị gián đoạn tại x=5
Đúng 2
Bình luận (0)
Xét tính liên tục của hàm số sau trên tập xác định của nó:
f
(
x
)
x
2
-
5
x
+
6
k
h
i
x
3...
Đọc tiếp
Xét tính liên tục của hàm số sau trên tập xác định của nó: f ( x ) = x 2 - 5 x + 6 k h i x > 3 2 x + 1 k h i x ≤ 3
Xét tính liên tục của hàm số sau trên tập xác định của nó:
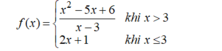
● Hàm số liên tục với mọi x ≠ 3.
● Tại x = 3, ta có:
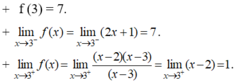
⇒ Hàm số không liên tục tại x = 3.
- Vậy hàm số liên tục trên các khoảng (-∞ ; 3), (3 ; +∞).
Đúng 0
Bình luận (0)
xét tính liên tục của hàm số sau tại x = 2
\(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{2x^2-7x+6}{2-x}\\2x-5\end{matrix}\right.\) khi \(x\ne2\); khi \(x=2\)
\(\lim\limits_{x\rightarrow2}f\left(x\right)=\lim\limits_{x\rightarrow2}\dfrac{2x^2-7x+6}{2-x}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{2x^2-4x-3x+6}{-\left(x-2\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(3-2x\right)}{x-2}=\lim\limits_{x\rightarrow2}3-2x=3-2\cdot2=3-4=-1\)
\(f\left(2\right)=2\cdot2-5=-1\)
=>\(\lim\limits_{x\rightarrow2}f\left(x\right)=f\left(2\right)\)
=>Hàm số liên tục tại x=2
Đúng 1
Bình luận (0)
Cho hàm số yf(x) liên tục trên R và có bảng xét dấu của hàm số f(x) như sau:Hàm số yf(x) đồng biến trên khoảng nào dưới đây ? A.(0;2) B.
1
;
+
∞
C.
0
;
+
∞
D.
-
∞
;...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và có bảng xét dấu của hàm số f'(x) như sau:

Hàm số y=f(x) đồng biến trên khoảng nào dưới đây ?
A.(0;2)
B. 1 ; + ∞
C. 0 ; + ∞
D. - ∞ ; 0
Xét tính liên tục của mỗi hàm số sau trên tập xác định của hàm số đó:
a) f(x)=x2+sinx;
b) g(x)=x4−x2+\(\dfrac{6}{x-1}\);
c) h(x)=`(2x)/(x−3)+(x−1)/(x+4)`.
a: TXĐ: D=R
x^2;sin x đều liên tục trên R
=>f(x) liên tục trên R
b: TXĐ: D=R\{1}
x^4;-x^2;6/x-1 đều liên tục khi x thuộc (-vô cực;1) hoặc (1;+vô cực)
=>g(x) liên tục trên (-vô cực;1) và (1;+vô cực)
c: ĐKXĐ: x<>3; x<>-4
HS \(\dfrac{2x}{x-3}\) liên tục trên (-vô cực;3) và (3;+vô cực)
(x-1)/(x+4) liên tục trên (-vô cực;-4) và (-4;+vô cực)
=>h(x) liên tục trên từng khoảng xác định của nó
Đúng 0
Bình luận (0)