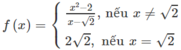
Tập xác định của hàm số là D = R
- Nếu x ≠ √2 thì 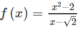
Đây là hàm phân thức hữu tỉ nên liên tục trên các khoảng (-∞; √2) và (√2; +∞)
- Tại x = √2:
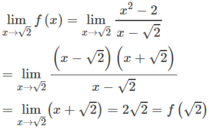
Vậy hàm số liên tục tại x = √2
Kết luận : y = f(x) liên tục trên R
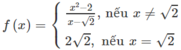
Tập xác định của hàm số là D = R
- Nếu x ≠ √2 thì 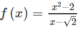
Đây là hàm phân thức hữu tỉ nên liên tục trên các khoảng (-∞; √2) và (√2; +∞)
- Tại x = √2:
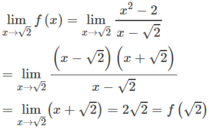
Vậy hàm số liên tục tại x = √2
Kết luận : y = f(x) liên tục trên R
Xét tính liên tục của các hàm số sau trên tập xác định của chúng g ( x ) = 1 - x x - 2 2 n ế u x ≠ 2 3 n ế u x = 2
Xét tính liên tục của các hàm số sau trên TXĐ của chúng
f(x)= {x2-3x +4 khi x<2
{ 5 khi x=2
{2x +1 khi x>2
Cho hàm số f x = 3 x + 2 n ế u x < - 1 x 2 - 1 n ế u x ≥ - 1
a. Vẽ đồ thị hàm số y= f(x). Từ đó nêu nhận xét vê tính liên tục của hàm số trên tập xác định của nó.
b. Khẳng định nhận xét trên bằng 1 chứng minh.
Xét tính liên tục của hàm số sau trên tập xác định của nó: f ( x ) = x 2 - 5 x + 6 k h i x > 3 2 x + 1 k h i x ≤ 3
Xét tính liên tục của mỗi hàm số sau trên tập xác định của hàm số đó:
a) f(x)=x2+sinx;
b) g(x)=x4−x2+\(\dfrac{6}{x-1}\);
c) h(x)=`(2x)/(x−3)+(x−1)/(x+4)`.
Xét tính liên tục của hàm số f ( x ) = x 2 + 5 x + 4 x 3 + 1 n ế u x ≠ - 1 1 n ế u x = 1 trên tập xác định của nó.
xét tính liên tục của hàm số sau trên R
\(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^2-4}{2-x}\\x-7\end{matrix}\right.\) khi \(x\ne2\); khi \(x=2\)
Xét tính liên tục của hàm số sau tại điểm x 0 = 2
f ( x ) = 2 x 2 - 3 x - 2 k h i x ≠ 2 3 2 k h i x = 2
Cho hàm số f ( x ) = 4 - x 2 - 2 ≤ x ≤ 2 1 x > 2 . Tìm khẳng định đúng trong các khẳng định sau:
(I) f(x) không xác định tại x = 3
(II) f(x) liên tục tại x = -2
(III) lim x → 2 f ( x ) = 2
A. Chỉ (I).
B. Chỉ (I) và (II).
C. Chỉ (I) và (III).
D. Cả (I); (II); (III) đều sai.