Cho hình 16. Hãy chứng minh rằng:
DE < BC.
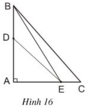
Cho hình 16 : Hãy chứng minh rằng :
a) BE < BC
b) DE < BC

a) Trong hình vẽ BE < BC là hai đường xiên vẽ từ B đến đường AC và AE, AC là hai hình chiếu của chúng vì AE < AC nên BE < BC
b) EB và ED là hai đường xiên vẽ từ E đến AB
AB và AD là hai hình chiếu của chúng
Vì AD < AB nên DE < BE
Ta có: BE < BC và DE < BE nên DE < BC
Cho hình 16. Hãy chứng minh rằng:
BE < BC;
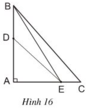
Ta có: BE, BC là hai đường xiên vẽ từ B đến đường AC.
BA ⏊ AC tại A nên A là hình chiếu của B trên AC
⇒ AE, AC lần lượt là hình chiếu của BE, BC trên AC.
Trong hình vẽ E nằm giữa A và C ⇒ AE < AC ⇒ BE < BC (đường xiên nào có hình chiếu lớn hơn thì lớn hơn).
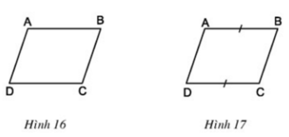
Hình thang ABCD có đáy AB, CD.
a) Cho biết AD // BC (h.16). Chứng minh rằng AD = BC, AB = CD.
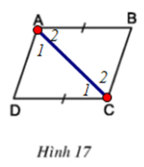
b) Cho biết AB = CD (h.17). Chứng minh rằng AD // BC, AD = BC.
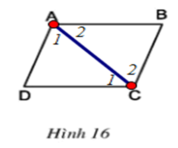
Hình thang ABCD có đáy AB, CD ⇒ AB // CD ⇒ ∠A2 = ∠C1 ̂ (hai góc so le trong)
Lại có: AD // BC ⇒ ∠A1 = ∠C2 (hai góc so le trong)
Xét ΔABC và ΔCDA có:
∠A2 = ∠C1 (cmt)
AC chung
∠A1 = ∠C2 (cmt)
⇒ ΔABC = ΔCDA (g.c.g)
⇒ AD = BC, AB = CD (các cặp cạnh tương ứng)
b)
Xét ΔABC và ΔCDA có:
AC chung
∠A2 = ∠C1 (cmt)
AB = CD
⇒ ΔABC = ΔCDA (c.g.c)
⇒ AD = BC (hai cạnh tương ứng)
∠A1 = ∠C2 (hai góc tương ứng) ⇒ AD // BC (hai góc so le trong bằng nhau)
Cho hình vuông ABCD. Trên cạnh AB lấy điểm E sao cho BE = 1
3 AB.
Đường thẳng DE cắt BC kéo dài tại K
a) Chứng minh rằng: ADE và BKE đồng dạng
b) Gọi H là hình chiếu của C lên DE. Chứng minh rằng: AD.HD = HC.AE
c) Tính diện tích tam giác CDK khi biết độ dài AB = 6cm
d) Chứng minh rằng: CH.KD = CD2 + CB.KB
ko làm mà đòi có ăn thì chỉ có ăn cứt và ăn đầu bồi nhá
Cho hình vẽ sau và biết rằng Ax song song với BC. a) Chứng minh rằng DE song song với BC. b) Tính số đo (theo độ) góc EOC.
Cho hình 16. Hãy chứng minh rằng: a) BE < BC b) DE < BC

AB \(\perp\) AC (gt)
Có E nằm giữa A và C
=> AE<AC
=> BE<BC ( qh giữa đg xiên và hình chiếu ) (1)
Có D nằm giữa A và B
=> AD<AB
=> DE<BE ( qh giữa đg xiên và hc ) (2)
Từ (1) và (2) => DE<BC
a) \(\widehat{BEC}\) là góc ngoài của tam giác vuông ABE nên \(\widehat{BEC}\) là góc tù.
Do đó, tam giác BEC có BE < BC (BE là cạnh đối diện với góc tù) (1)
b) Ta có: AD, AB lần lượt là hình chiếu của ED, EB lên đường thẳng AB. Vì AD < AB => ED < EB (2)
Từ (1) và (2) ta có: DE < BC
Cho tam giác ABC, phân giác của góc b và góc c cắt AC và AB tại D và E.
1, Chứng minh rằng: AD bằng AE, DE//BC
2,Biết DE BẰNG 10cm, BC bằng 16 cm. tính ab bằng ?
Cho ABC vuông tại A , phân giác BD ( D AC ). Kẻ DE BC ( E BC ). a) Chứng minh rằng ABD EBD . b) Kẻ AH BC ( H BC ), AH cắt BD tại I . Chứng minh rằng AH DE và AID cân. c) Chứng minh rằng AE là phân giác của HAC . d) ABC cần có thêm điều kiện gì để DC AI
Cho hình bình hành ABCD.gọi E là trung điểm của AD,Flà trung điểm của BC . Chứng minh rằng :BE=DE