Cho sina = 3/5 với 0 0 < a < 90 0 . Khi đó tana bằng:

Những câu hỏi liên quan
cho 0<a<45 cmr:a)sina<cosa b)tana<cota
Cho sina =0, 28 tính cosa,tana,cota
Lời giải:
Do góc $a$ nhọn nên các tỉ số lượng giác mang giá trị dương.
Áp dụng công thức $\sin ^2a+\cos ^2a=1$
$\Rightarrow \cos^2 a=1-\sin ^2a=1-0,28^2=0,9216$
$\Rightarrow \cos a=\frac{24}{25}=0,96$
$\tan a=\frac{\sin a}{\cos a}=\frac{0,28}{0,96}=\frac{7}{24}$
$\cot a=\frac{1}{\tan a}=\frac{24}{7}$
Cho
tan
a
12
với
a
∈
π
;
3
π
2
Khi đó sina bằng A.
1
145
B.
-
1
145
C.
12
145...
Đọc tiếp
Cho tan a = 12 với a ∈ π ; 3 π 2 Khi đó sina bằng
A. 1 145
B. - 1 145
C. 12 145
D. - 12 145
Ta có tan α . c ot α = 1 ⇒ 12. cot α = 1 ⇔ cot α = 1 12
Lại có 1 sin 2 α = 1 + cot 2 α = 1 + 1 144 = 145 144 ⇔ sin 2 α = 144 145
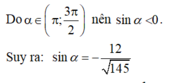
Đáp án D
Đúng 0
Bình luận (0)
a) Tính: cosA, sinA, biết tanA= \(\dfrac{3}{5}\)
b) Tính: sinA, tanA, biết cosA=\(\dfrac{1}{4}\)
MỌI NGƯỜI GIÚP EM VỚI Ạ. EM CẢM ƠN NHIỀU Ạ
a) Có: `1+tan^2a=1/(cos^2a)`
`<=> 1+(3/5)^2=1/(cos^2a)`
`=> cosa=\sqrt10/4`
`=> sina = \sqrt(1-cos^2a) = \sqrt6/4`
b) Có: `sin^2a + cos^2a=1`
`<=> sin^2a + (1/4)^2=1`
`=> sina=\sqrt15/4`
`=> tana = (sina)/(cosa) = \sqrt15`
Đúng 1
Bình luận (3)
a) Giả sử tam giác ABC vuông tại B có \(tanA=\dfrac{3}{5}\)
\(\Rightarrow\dfrac{BC}{AB}=\dfrac{3}{5}\Rightarrow BC=\dfrac{3}{5}AB\Rightarrow AC=\sqrt{AB^2+\dfrac{9}{25}AB^2}=\dfrac{\sqrt{34}}{5}AB\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{5}{\sqrt{34}}\Rightarrow cosA=\dfrac{5}{\sqrt{34}}\)
\(AC=\dfrac{\sqrt{34}}{5}AB\Rightarrow AC=\dfrac{\sqrt{34}}{5}.\dfrac{5}{3}BC=\dfrac{\sqrt{34}}{3}BC\Rightarrow\dfrac{BC}{AC}=\dfrac{3}{\sqrt{34}}\)
\(\Rightarrow sinA=\dfrac{3}{\sqrt{34}}\)
b) cũng tương tự như câu a thôi,bạn tự tính nha
Đúng 1
Bình luận (0)
câu20:Cho tana=-2 và pi/2<a<pi.Tính giá trị biểu thức P=cos2a+sin2a
câu21Cho 2tana-cota=1 và -pi/2<a<0.Tính giá trị của biểu thức P=tana+2cota
câu22: Cho sina=-1/7 và pi<a<3pi/2.Tính giá trị của biểu thức P=cos(a+pi/6)
câu23: Cho sina=-1/9; cosb=-2/3 và pi<a<3pi/2; pi/2<b<pi. Tính giá trị của biểu thức P= sin(a+b)
tìm cotA biết sinA+cosA=7/5 (0<A<90)
Ta có \(\sin A=1,4-\cos A\)
Thế vào \(\sin^2A+\cos^2A=1\)ta được
\(25\cos^2A-35\cos A+12=0\)
\(\Leftrightarrow\orbr{\begin{cases}\cos A=0,8\\\cos A=0,6\end{cases}\Rightarrow\orbr{\begin{cases}\sin A=0,6\\\sin A=0,8\end{cases}}}\)
\(\Rightarrow\orbr{\begin{cases}\cot A=\frac{4}{3}\\\cot A=\frac{3}{5}\end{cases}}\)
Đúng 0
Bình luận (0)
giả sử tam giác ABC vuông tại A
đặt Ab=c; AC=b; BC=a, \(\widehat{B}\)=A
ta có:
\(sinA+cosA=\frac{b}{a}+\frac{c}{a}=\frac{b+c}{a}=\frac{7}{5}\)
=>b+c=7
=>(b+c)2=b2+2bc+c2=49
=>\(sin^2A+cos^2A=\left(\frac{b}{a}\right)^2+\left(\frac{c}{a}\right)^2=\frac{b^2+c^2}{a^2}=\frac{a^2}{a^2}=\frac{25}{25}\)
=>b2+c2=25
ta có:
(b+c)2-b2-c2=49-25
2bc=24
bc=12
ta có: b.c=12; b+c=7
=> 3.4=4.3=1.12=12.1=2.6=6.2
mà b+c=7=> b=4,c=3 hoặc b=3,c=4
=> cot A= 4/3 hoặc 3/4
Đúng 0
Bình luận (0)
Cho tana=\(\dfrac{1}{3}\)Tính\(\dfrac{cosa-sina}{cosa+sina}\)
Chứng minh rằng:\(\dfrac{1-tana}{1+tana}=\dfrac{cosa-sina}{cosa+sina}\)
cho tam giác abc có 3 góc nhọn. Vẽ đường cáo AD, BE, CF cắt nhau tại H. Chứng minh:
a) \(0< cos^2A+cos^2B+cos^2C< 1\)
b)\(2< sin^2A+sin^2B+sin^2C< 3\)
c)sinA + sinB + sinC < 2( cosA + cosB + cosC)
d)sinB . cosC + sinC . cosB = sinA
e)tanA + tanB + tanC = tanA . tanB . tanC
Tính giá trị các biểu thức:
Afrac{cota+tana}{cota-tana}biết sinafrac{3}{5}và 0afrac{pi}{2}
Cho tan a3.Tínhfrac{2sina+3cosa}{4sina-5cosa}
Cho cot a3 tính giá trị biểu thức:Afrac{2sin^2a-3cos^2a}{sin^2a-2sina.cosa-cos^2a}
MỌI NGƯỜI GIÚP MÌNH VỚI.MÌNH CẢM ƠN NHIỀU
Đọc tiếp
Tính giá trị các biểu thức:
\(A=\frac{cota+tana}{cota-tana}\)biết sina=\(\frac{3}{5}\)và 0<a<\(\frac{\pi}{2}\)
Cho tan a=3.Tính\(\frac{2sina+3cosa}{4sina-5cosa}\)
Cho cot a=3 tính giá trị biểu thức:A=\(\frac{2sin^2a-3cos^2a}{sin^2a-2sina.cosa-cos^2a}\)
MỌI NGƯỜI GIÚP MÌNH VỚI.MÌNH CẢM ƠN NHIỀU
\(0< a< \frac{\pi}{2}\Rightarrow cosa>0\Rightarrow cosa=\sqrt{1-sin^2a}=\frac{4}{5}\)
\(\Rightarrow tana=\frac{sina}{cosa}=\frac{3}{4}\) ; \(cota=\frac{1}{tana}=\frac{4}{3}\)
\(\Rightarrow A=\frac{\frac{4}{3}+\frac{3}{4}}{\frac{4}{3}-\frac{3}{4}}=...\)
\(\frac{2sina+3cosa}{4sina-5cosa}=\frac{\frac{2sina}{cosa}+\frac{3cosa}{cosa}}{\frac{4sina}{cosa}-\frac{5cosa}{cosa}}=\frac{2tana+3}{4tana-5}=\frac{2.3+3}{4.3-5}=...\)
\(A=\frac{2sin^2a-3cos^2a}{sin^2a-2sina.cosa-cos^2a}=\frac{\frac{2sin^2a}{sin^2a}-\frac{3cos^2a}{sin^2a}}{\frac{sin^2a}{sin^2a}-\frac{2sina.cosa}{sin^2a}-\frac{cos^2a}{sin^2a}}=\frac{2-3cot^2a}{1-2cota-cot^2a}=\frac{2-3.3^2}{1-2.3-3^2}=...\)
Đúng 0
Bình luận (0)


















