Giải hệ phương trình 2 x = 4 x + y = 5

Những câu hỏi liên quan
1. Giải phương trình: \(\sqrt{x-2}+\sqrt{4-x}=\sqrt{2}\) .
2. Giải phương trình: \(4x^4-7x^3+9x^2-10x+4=0\).
3. Giải hệ phương trình: \(\left\{{}\begin{matrix}x^2+y^2=3-xy\\x^4+y^4=2\end{matrix}\right.\) .
Bài 1: ĐKXĐ: $2\leq x\leq 4$
PT $\Leftrightarrow (\sqrt{x-2}+\sqrt{4-x})^2=2$
$\Leftrightarrow 2+2\sqrt{(x-2)(4-x)}=2$
$\Leftrightarrow (x-2)(4-x)=0$
$\Leftrightarrow x-2=0$ hoặc $4-x=0$
$\Leftrightarrow x=2$ hoặc $x=4$ (tm)
Đúng 2
Bình luận (0)
Bài 2:
PT $\Leftrightarrow 4x^3(x-1)-3x^2(x-1)+6x(x-1)-4(x-1)=0$
$\Leftrightarrow (x-1)(4x^3-3x^2+6x-4)=0$
$\Leftrightarrow x=1$ hoặc $4x^3-3x^2+6x-4=0$
Với $4x^3-3x^2+6x-4=0(*)$
Đặt $x=t+\frac{1}{4}$ thì pt $(*)$ trở thành:
$4t^3+\frac{21}{4}t-\frac{21}{8}=0$
Đặt $t=m-\frac{7}{16m}$ thì pt trở thành:
$4m^3-\frac{343}{1024m^3}-\frac{21}{8}=0$
$\Leftrightarrow 4096m^6-2688m^3-343=0$
Coi đây là pt bậc 2 ẩn $m^3$ và giải ta thu được \(m=\frac{\sqrt[3]{49}}{4}\) hoặc \(m=\frac{-\sqrt[3]{7}}{4}\)
Khi đó ta thu được \(x=\frac{1}{4}(1-\sqrt[3]{7}+\sqrt[3]{49})\)
Đúng 2
Bình luận (0)
Nãy mình tìm được một cách giải tương tự cho câu 2.
PT \(\Leftrightarrow\left(x-1\right)\left(4x^3-3x^2+6x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\4x^3-3x^2+6x-4=0\left(1\right)\end{matrix}\right.\)
Vậy pt có 1 nghiệm bằng 1.
\(\left(1\right)\Rightarrow8x^3-6x^2+12x-8=0\)
\(\Leftrightarrow7x^3+x^3-6x^2+12x-8=0\)
\(\Leftrightarrow\left(x-2\right)^3=-7x^3\)
\(\Leftrightarrow x-2=-\sqrt[3]{7}x\)
\(\Leftrightarrow x=\dfrac{2}{1+\sqrt[3]{7}}\)
Vậy pt có nghiệm \(S=\left\{1;\dfrac{2}{1+\sqrt[3]{7}}\right\}\)
Lưu ý: Nghiệm của người kia hoàn toàn tương đồng với nghiệm của mình (\(\dfrac{2}{1+\sqrt[3]{7}}=\dfrac{1}{4}\left(1-\sqrt[3]{7}+\sqrt[3]{49}\right)\))
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hệ phương trình: 2X +Y = 3m-2 ( m là tham số ) X - Y = 5 a) Giải hệ phương trình khi m = - 4 ; b) Tìm m để hệ phương trình có nghiệm (x; y) thỏa mãn: x + y = 13.
1) Giải hệ phương trình $\left\{\begin{array}{l}2 x+y=19 \\ 3 x-2 y=11\end{array}\right.$.
2) Giải phương trình $x^{2}+20 x-21=0$.
3) Giải phương trình $x^{4}-20 x^{2}+64=0$.
3(2x+y)-2(3x-2y)=3.19-11.2
6x+3y-6x+4y=57-22
7y=35
y=5
thay vào :
2x+y=19
2x+5=19
2x=14
x=7
2/ x2+21x-1x-21=0
x(x+21)-1(x+21)=0
(x+21)(x-1)=0
TH1 x+21=0
x=-21
TH2 x-1=0
x=1
vậy x = {-21} ; {1}
3/ x4-16x2-4x2+64=0
x2(x2-16)-4(x2-16)=0
(x2-16)-(x2-4)=0
TH1 x2-16=0
x2=16
<=>x=4;-4
TH2 x2-4=0
x2=4
x=2;-2
Bài 1 :
\(\hept{\begin{cases}2x+y=19\\3x-2y=11\end{cases}\Leftrightarrow\hept{\begin{cases}4x+2y=38\\3x-2y=11\end{cases}\Leftrightarrow\hept{\begin{cases}7x=49\\2x+y=19\end{cases}}}}\)
\(\Leftrightarrow\hept{\begin{cases}x=7\\2x+y=19\end{cases}}\)Thay vào x = 7 vào pt 2 ta được :
\(14+y=19\Leftrightarrow y=5\)Vậy hệ pt có một nghiệm ( x ; y ) = ( 7 ; 5 )
Bài 2 :
\(x^2+20x-21=0\)
\(\Delta=400-4\left(-21\right)=400+84=484\)
\(x_1=\frac{-20-22}{2}=-24;x_2=\frac{-20+22}{2}=1\)
Bài 3 : Đặt \(x^2=t\left(t\ge0\right)\)
\(t^2-20t+64=0\)
\(\Delta=400+4.64=656\)
\(t_1=\frac{20+4\sqrt{41}}{2}\left(tm\right);t_2=\frac{20-4\sqrt{41}}{2}\left(ktm\right)\)
Theo cách đặt : \(x^2=\frac{20+4\sqrt{41}}{2}\Rightarrow x=\sqrt{\frac{20+4\sqrt{41}}{2}}=\frac{\sqrt{20\sqrt{2}+4\sqrt{82}}}{2}\)
\(\hept{\begin{cases}2x+y=19\\3x-2y=11\end{cases}\hept{\begin{cases}6x+3y=57\\6x-4y=22\end{cases}\hept{\begin{cases}7y=35\\3x-2y=11\end{cases}}}}\)
\(\hept{\begin{cases}y=5\\3x-2.5=11\end{cases}\hept{\begin{cases}y=5\\3x=21\end{cases}\hept{\begin{cases}y=5\\x=7\end{cases}}}}\)
\(a=1,b=20;c=-21\)
\(\Delta=\left(20\right)^2-\left(4.1.-21\right)=484\)
\(\sqrt{\Delta}=\sqrt{484}=22\)
\(x_1=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-20+22}{2}=1\left(TM\right)\)
\(x_2=\frac{-b-\sqrt{\Delta}}{2a}=-21\left(TM\right)\)
\(3,x^4-20x^2+64=0\)
đặt \(x^2=a\)ta có pt
\(a^2-20a+64=0\)
\(a=1;b=-20;c=64\)
\(\Delta=\left(-20\right)^2-\left(4.1.64\right)=144\)
\(\sqrt{\Delta}=12\)
\(a_1=\frac{-b+\sqrt{\Delta}}{2a}=16\left(TM\right)\)
\(a_2=\frac{-b-\sqrt{\Delta}}{2a}=4\left(TM\right)\)
\(< =>x_1=\sqrt{16}=4\left(TM\right)\)
\(x_2=\sqrt{4}=2\left(TM\right)\)
vậy bộ n0 của pt là (\(4;2\))
Xem thêm câu trả lời
1) Giải hệ phương phương trình trình 1/(x - 2) - 2sqrt(y + 1) = - 4; 2/(x - 2) + sqrt(y + 1) = 7
ĐKXĐ: x<>2 và y>=-1
\(\left\{{}\begin{matrix}\dfrac{1}{x-2}-2\sqrt{y+1}=-4\\\dfrac{2}{x-2}+\sqrt{y+1}=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{2}{x-2}-4\sqrt{y+1}=-8\\\dfrac{2}{x-2}+\sqrt{y+1}=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-5\sqrt{y+1}=-15\\\dfrac{2}{x-2}+\sqrt{y+1}=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\sqrt{y+1}=3\\\dfrac{2}{x-2}=7-3=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y+1=9\\x-2=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=8\\x=\dfrac{5}{2}\end{matrix}\right.\left(nhận\right)\)
Đúng 1
Bình luận (0)
giải hệ phương trình: x^2+2x+3=(x^2+x+1)(x^4+x^2+4)
giải hệ phương trình: x^2+2x+3=(x^2+x+1)(x^4+x^2+4)
Bài 1:Cho biểu thức P=√x + 1/√x - 2 + 2√x/√x +2 + 2+5√x /4-x
a)Rút gọn P
b)Tìm x để P=2
Bài 2:Cho hệ phương trình x+my=9 và mx-3y=4
a)Giải hệ phương trình với m=3
b)Tìm m để hệ phương trính có nghiệm x=-1,y=3
Bài 1:
a) Ta có: \(P=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{2+5\sqrt{x}}{4-x}\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\cdot\left(\sqrt{x}+2\right)}+\dfrac{2\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}-\dfrac{2+5\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)
b)
ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne4\end{matrix}\right.\)
Để P=2 thì \(\dfrac{3\sqrt{x}}{\sqrt{x}+2}=2\)
\(\Leftrightarrow3\sqrt{x}=2\left(\sqrt{x}+2\right)\)
\(\Leftrightarrow3\sqrt{x}=2\sqrt{x}+4\)
\(\Leftrightarrow3\sqrt{x}-2\sqrt{x}=4\)
\(\Leftrightarrow\sqrt{x}=4\)
hay x=16(nhận)
Vậy: Để P=2 thì x=16
Đúng 2
Bình luận (0)
2.
a, \(m=3\), hệ phương trình trở thành:
\(\left\{{}\begin{matrix}x+3y=9\\3x-3y=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x=13\\y=\dfrac{3x-4}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{13}{4}\\y=\dfrac{23}{12}\end{matrix}\right.\)
b, \(\left(x;y\right)=\left(-1;3\right)\) là nghiệm của hệ, suy ra:
\(\left\{{}\begin{matrix}-1+3m=9\\-m-9=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{10}{3}\\m=-13\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại giá trị m thỏa mãn
Đúng 2
Bình luận (0)
giải hệ phương trình sau
{ 2(x + y) + 3(x - y) = 4
{ (x + y) + 2(x - y) = 5
\(\Leftrightarrow\left\{{}\begin{matrix}2\left(x+y\right)+3\left(x-y\right)=4\\2\left(x+y\right)+4\left(x-y\right)=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y=6\\2\left(x+y\right)+24=10\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x-y=6\\x+y=-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=-\dfrac{13}{2}\end{matrix}\right.\)
Đúng 3
Bình luận (0)
a. Giải phương trình: $x^2 - 3x + 2 = 0$.
b. Giải hệ phương trình: $\left\{ \begin{aligned} & x + 3y = 3\\ & 4 x - 3 y = -18 \end{aligned}\right.$.
c. Rút gọn biểu thức: $A = \dfrac2{2+\sqrt7}+\dfrac{\sqrt{28}}2 - 2$.
d. Giải phương trình: $(x^2 - 2x)^2 + (x-1)^2 - 13 = 0.$
a) x^2 - 3x + 2 = 0
\(\Delta=b^2-4ac=\left(-3\right)^2-4.1.2=1\)
=> pt có 2 nghiệm pb
\(x_1=\frac{-\left(-3\right)+1}{2}=2\)
\(x_2=\frac{-\left(-3\right)-1}{2}=1\)
a) Dễ thấy phương trình có a + b + c = 0
nên pt đã cho có hai nghiệm phân biệt x1 = 1 ; x2 = c/a = 2
b) \(\hept{\begin{cases}x+3y=3\left(I\right)\\4x-3y=-18\left(II\right)\end{cases}}\)
Lấy (I) + (II) theo vế => 5x = -15 <=> x = -3
Thay x = -3 vào (I) => -3 + 3y = 3 => y = 2
Vậy pt có nghiệm ( x ; y ) = ( -3 ; 2 )
a, x1 = 1 , x2 = 2
b, x = -3 , y = 2
c, A = 1
d, x = -1 , x= 3
Giải các hệ phương trình sau:
{ (x - 5)(y - 2) = (x + 2)(y - 1)
{ (x - 4)(y + 7) = (x - 3)(y + 4)
\(\left\{{}\begin{matrix}\left(x-5\right)\left(y-2\right)=\left(x+2\right)\left(y-1\right)\\\left(x-4\right)\left(y+7\right)=\left(x-3\right)\left(y+4\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy-2x-5y+10=xy-x+2y-2\\xy+7x-4y-28=xy+4x-3y-12\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+7y=12\\3x-y=16\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x+21y=36\\3x-y=16\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}22y=20\\x+7y=12\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{62}{11}\\y=\dfrac{10}{11}\end{matrix}\right.\)
Đúng 2
Bình luận (0)







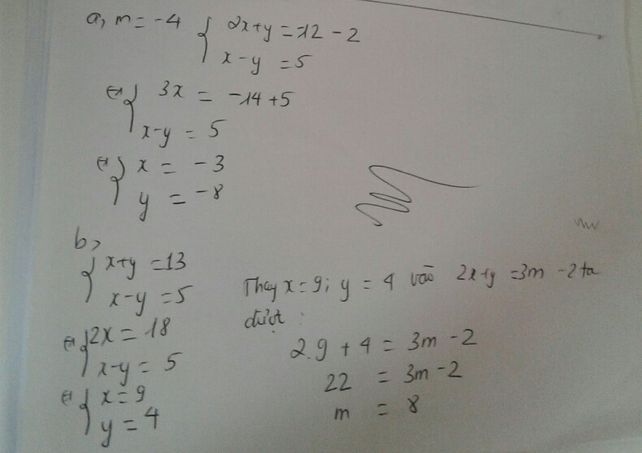 Bn tham khảo nhé!
Bn tham khảo nhé!




















