TAM GIÁC ABC VUÔNG TẠI A. GÓC B CÓ SỐ ĐO LÀ 60 ĐỘ. BA=4.5CM. TÍNH BC

Những câu hỏi liên quan
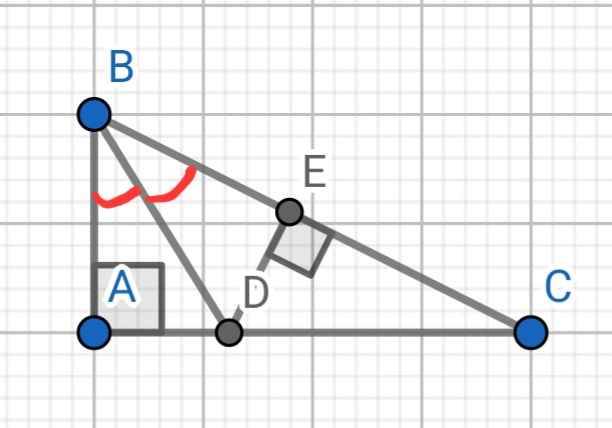
Tam giác ABC vuông tại A, có góc B= 60 độ. Tia phân giác của góc B cắt AC ở D. Từ D kẻ DE vuông góc với BC tại E
a) Chứng minh rằng BA=BE
b) Tính số đo góc EDC
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>BA=BE
b: góc ADE=180-60=120 độ
=>góc EDC=60 độ
Đúng 1
Bình luận (0)
Tam giác ABC vuông tại A, có góc B=60 độ. Tia phân giác của góc B cắt AC ở D. Từ D kẻ DE vuông góc với BC tại E
a) chứng minh rằng: BA=BE
b) tính số đo góc EDC
a) Xét hai tam giác vuông: ∆ABD và ∆EBD có:
∠ABD = ∠EBD (BD là phân giác của B)
BD chung
⇒ ∆ABD = ∆EBD (cạnh huyền - góc nhọn)
⇒ BA = BE (hai cạnh tương ứng)
b) Do ∆ABC vuông tại A
⇒ ∠B + ∠C = 90⁰
⇒ ∠C = 90⁰ - ∠B
= 90⁰ - 60⁰
= 30⁰
∆DEC vuông tại E có
∠C = 30⁰
∠EDC + ∠C = 90⁰
⇒ ∠EDC = 90⁰ - ∠C
= 90⁰ - 30⁰
= 60⁰
Đúng 1
Bình luận (2)
cho tam giác abc vuông tại a có góc b = 60 độ. trên bc lấy điểm h sao cho hb = ba, từ h kẻ he vuông góc bc tại h (e thuộc ac)
a) tính số đo góc C
b) chứng minh be là tia phân giác góc b
c) gọi k là giao điểm của ba và he. chứng minh rằng be vuông góc với kc
a: góc C=90-60=30 độ
b: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
BA=BH
=>ΔBAE=ΔBHE
=>góc ABE=góc HBE
=>BE là phân giác của góc ABC
c: Xét ΔEAK vuông tại A và ΔEHC vuông tại H có
EA=EH
góc AEK=góc HEC
=>ΔEAK=ΔEHC
=>EK=EC và AK=HC
mà BA=BH
nên BK=BC
mà EK=EC
nên BE là trung trực của KC
=>BE vuong góc KC
Đúng 2
Bình luận (0)
Tam giác ABC vuông tại A có góc B = 60 độ,AB=3cm. AM là đường trung tuyến của tam giác. Tính độ dài cạnh BC và số đo góc MAC?
cho tam giác ABC vuông tại A có góc B = 60 độ
a, tính số đo góc C
b, trên cạnh BC lấy điểm E sao cho BE = BA ,tia phân giác của góc B cắt AC tại D. Chứng minh DE vuông góc với BC
c, đường thẳng DE cắt đường thẳng ABc tại I, BD cắt IC tại K. Chứng minh K là trung điểm của IC
a: \(\widehat{C}=90^0-60^0=30^0\)
b: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: \(\widehat{BAD}=\widehat{BED}=90^0\)
hay DE⊥CB
Đúng 1
Bình luận (1)
Cho tam giác ABC vuông tại A có góc B 60 độa)Tính số đo góc C và so sánh độ dài 3 cạnh của tam giác ABC.b)Vẽ BD là tia phân giác của góc ABC (D thuộc AC). Qua D vẽ DK vuông góc với BC (K thuộc BC). Chứng minh tam giác BADtam giác BKD.c)Chứng minh tam giác BDC cân và K là trung điểm BC.d)Tia KD cắt BA tại I. Tính độ dài cạnh ID biết AB3cm (làm tròn kết quả đến chữ số thập phân thứ nhất).
Đọc tiếp
Cho tam giác ABC vuông tại A có góc B = 60 độ
a)Tính số đo góc C và so sánh độ dài 3 cạnh của tam giác ABC.
b)Vẽ BD là tia phân giác của góc ABC (D thuộc AC). Qua D vẽ DK vuông góc với BC (K thuộc BC). Chứng minh tam giác BAD=tam giác BKD.
c)Chứng minh tam giác BDC cân và K là trung điểm BC.
d)Tia KD cắt BA tại I. Tính độ dài cạnh ID biết AB=3cm (làm tròn kết quả đến chữ số thập phân thứ nhất).
GIÚP MÌNH VỚI CÁC BẠN ƠI!!!
ARIGATO!!!
Cho tam giác ABC vuông tại A, có góc ABC = 60*. Trên tia BC lấy điểm D sao cho BD = BA. Đường thẳng vuông góc với BC tại D cắt cạnh AC tại E, cắt tia BA tại F.
a) Tính số đo góc ACB và so sánh độ dài các cạnh của tam giác ABC.
b) Chứng minh: BE là đường trung trực của đoạn thẳng AD và BE là tia phân giác của góc ABC.
c) Chúng minh: AD // FC.
d) Chứng minh: AC = 3DE.
Bài làm
a) Xét tam ABC vuông tại A có:
\(\widehat{ACB}+\widehat{ABC}=90^0\)( hai góc phụ nhau )
hay \(\widehat{ACB}+60^0=90^0\)
=> \(\widehat{ACB}=90^0-60^0=30^0\)
b) Xét tam giác ABE và tam giác DBE có:
\(\widehat{BAE}=\widehat{BDE}=90^0\)
Cạnh huyền: BE chung
Cạnh góc vuông: AB = BD ( gt )
=> Tam giác ABE = tam giác DBE ( cạnh huyền - cạnh góc vuông )
=> \(\widehat{ABE}=\widehat{DBE}\)( hai góc tương ứng )
=> BI là tia phân giác của góc BAC
Mà I thược BE
=> BE là tia phân giác của góc BAC
Gọi I là giao điểm BE và AD
Xét tam giác AIB và tam giác DIB có:
AB = BD ( gt )
\(\widehat{ABE}=\widehat{DBE}\)( cmt )
BI chung
=> Tam giác AIB = tam giác DIB ( c.g.c )
=> AI = ID (1)
=> \(\widehat{BIA}=\widehat{BID}\)
Ta có: \(\widehat{BIA}+\widehat{BID}=180^0\)( hai góc kề bù )
Hay \(\widehat{BIA}=\widehat{BID}=\frac{180^0}{2}=90^0\)
=> BI vuông góc với AD tại I (2)
Từ (1) và (2) => BI là đường trung trực của đoạn AD
Mà I thược BE
=> BE là đường trung trực của đoạn AD ( đpcm )
c) Vì tam giác ABE = tam giác DBE ( cmt )
=> AE = ED ( hai cạnh tương ứng )
Xét tam giác AEF và tam giác DEC có:
\(\widehat{EAF}=\widehat{EDC}=90^0\)
AE = ED ( cmt )
\(\widehat{AEF}=\widehat{DEF}\)( hai góc đối )
=> Tam giác AEF = tam giác DEC ( g.c.g )
=> AF = DC
Ta có: AF + AB = BF
DC + BD = BC
Mà AF = DC ( cmt )
AB = BD ( gt )
=> BF = BC
=> Tam giác BFC cân tại B
=> \(\widehat{BFC}=\widehat{BCF}=\frac{180^0-\widehat{FBC}}{2}\) (3)
Vì tam giác BAD cân tại B ( cmt )
=> \(\widehat{BAD}=\widehat{BDA}=\frac{180^0-\widehat{FBC}}{2}\) (4)
Từ (3) và (4) => \(\widehat{BAD}=\widehat{BFC}\)
Mà Hai góc này ở vị trí đồng vị
=> AD // FC
d) Xét tam giác ABC vuông tại A có:
\(\widehat{ACB}+\widehat{ABC}=90^0\)( hai góc phụ nhau ) (5)
Xét tam giác DEC vuông tại D có:
\(\widehat{DEC}+\widehat{ACB}=90^0\)( hai góc phụ nhau ) (6)
Từ (5) và (6) => \(\widehat{ABC}=\widehat{DEC}\)
Ta lại có:
\(\widehat{ABC}>\widehat{EBC}\)
=> AC > EC
Mà \(\widehat{EBC}=\frac{1}{2}\widehat{ABC}\)
=> EC = 1/2 AC.
=> E là trung điểm AC
Mà EC = EF ( do tam giác AEF = tam giác EDC )
=> EF = 1/2AC
=> AE = EC = EF
Và AE = ED ( cmt )
=> ED = EC
Mà EC = 1/2AC ( cmt )
=> ED = 1/2AC
=> 2ED = AC ( đpcm )
Mình chứng minh ra kiểu này cơ. không biết đề đúng hay sai!??
Cho tam giác ABC vuông tại A có, góc B= 60 độ và BC=2AB 1. Tính số đo góc C 2.Tia phân giác của góc B cắt cạnh AC tại điểm Đ. Trên đoạn thẳngBC lấy điểm H sao cho BH=BA. Chứng minh: tam giác ABD=tam giác HBD 3. Chứng minh DH là đường trung trực của BC
Cho Tam giác ABC vuông tại góc A, góc B=60 độ. Vẽ AH vuông góc với BC vuông tại H
Tính số đo góc HAc
Lời giải:
Ta thấy:
Xét tam giác vuông tại $H$ là $ABH$ có $\widehat{B}+\widehat{BAH}=90^0$
Xét tam giác vuông $BAC$ có: $\widehat{BAH}+\widehat{HAC}=\widehat{BAC}=90^0$
$\Rightarrow \widehat{B}+\widehat{BAH} = \widehat{BAH}+\widehat{HAC}$
$\Rightarrow \widehat{HAC}=\widehat{B}=60^0$
Đúng 0
Bình luận (0)














