\(1,\dfrac{x-1}{3}=x+1\\ \Leftrightarrow x-1=3x+3\\ \Leftrightarrow3x-x=3+1\\ \Leftrightarrow x=2\)

PT có tập nghiệm S = {2}

\(2,\sqrt{16x^2+8x+1}-2=x\\ \Leftrightarrow\sqrt{\left(4x+1\right)^2}-2=x\\\Leftrightarrow 4x+1-2=x\\ \Leftrightarrow4x-x=2-1\\ \Leftrightarrow x=\dfrac{1}{3}\)

PT có tập nghiệm S = {1/3}

\(3,\left\{{}\begin{matrix}2x+y=17\\x-2y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+y=17\\2x-4y=2\end{matrix}\right.\\ \Leftrightarrow\left(2x+y\right)-\left(2x-4y\right)=17-2\\ \Leftrightarrow5y=15\\ \Leftrightarrow y=3\\ \Leftrightarrow2x+3=17\\ \Leftrightarrow2x=14\\ \Leftrightarrow x=7\)

PTHH có tập nghiệm (x; y) là (7; 3)

\(\left\{{}\begin{matrix}\left(x-5\right)\left(y-2\right)=\left(x+2\right)\left(y-1\right)\\\left(x-4\right)\left(y+7\right)=\left(x-3\right)\left(y+4\right)\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}xy-2x-5y+10=xy-x+2y-2\\xy+7x-4y-28=xy+4x-3y-12\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x+7y=12\\3x-y=16\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x+21y=36\\3x-y=16\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}22y=20\\x+7y=12\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{62}{11}\\y=\dfrac{10}{11}\end{matrix}\right.\)

Bài toán giải hệ phương trình bằng phương pháp thế có 2 cách trình bày.

Cách 1:

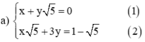
Từ (1) ta rút ra được x = -y√5 (*)

Thế (*) vào phương trình (2) ta được :

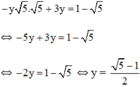
Thay y = 5 - 1 2 vào (*) ta được:  x = − 5 − 1 2 ⋅ 5 = 5 − 5 2

Vậy hệ phương trình có nghiệm  5 − 5 2 ; 5 − 1 2

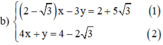
Từ (2) ta rút ra được y = -4x + 4 - 2 √3 (*)

Thế (*) vào phương trình (1) ta được:

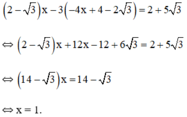
Thay x = 1 vào (*) ta được y = -4.1 + 4 - 2√3 = -2√3

Vậy hệ phương trình có nghiệm duy nhất (1; -2√3)

Cách 2 :

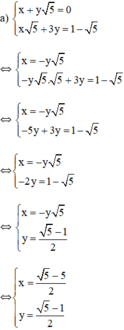
Vậy hệ phương trình có nghiệm duy nhất  5 − 5 2 ; 5 − 1 2

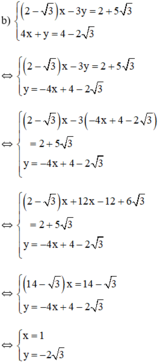
Vậy hệ phương trình có nghiệm duy nhất (1; -2√3)

Kiến thức áp dụng

Giải hệ phương trình 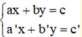 ta làm như sau:

Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn).

Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương .

Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.

3:

a: u+v=14 và uv=40

=>u,v là nghiệm của pt là x^2-14x+40=0

=>x=4 hoặc x=10

=>(u,v)=(4;10) hoặc (u,v)=(10;4)

b: u+v=-7 và uv=12

=>u,v là các nghiệm của pt:

x^2+7x+12=0

=>x=-3 hoặc x=-4

=>(u,v)=(-3;-4) hoặc (u,v)=(-4;-3)

c; u+v=-5 và uv=-24

=>u,v  là các nghiệm của phương trình:

x^2+5x-24=0

=>x=-8 hoặc x=3

=>(u,v)=(-8;3) hoặc (u,v)=(3;-8)

a) 3 x 2  – 7x + 2 = 0

Δ= 7 2  -4.3.2 = 49 - 24 = 25 > 0 ⇒ ∆ = 5

Phương trình có 2 nghiệm phân biệt:

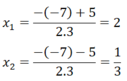
Vậy tập nghiệm của phương trình là S = {2; 1/3}

x = 2 2 x - y = 3

Đường thẳng (d): x = 2 song song với trục tung.

Đường thẳng (d’): 2x – y = 3 không song song với trục tung

⇒ (d) cắt (d’)

⇒ Hệ có nghiệm duy nhất.

Vẽ (d): x = 2 là đường thẳng đi qua (2 ; 0) và song song với trục tung.

Vẽ (d’): 2x - y = 3

- Cho x = 0 ⇒ y = -3 được điểm (0; -3).

- Cho y = 0 ⇒ x = 1,5 được điểm (1,5 ; 0).

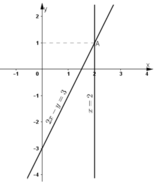
Ta thấy hai đường thẳng (d) và (d’) cắt nhau tại A(2; 1).

Vậy hệ phương trình có nghiệm (2; 1).

Bài toán này có hai cách giải:

Cách 1: Thu gọn từng phương trình ta sẽ thu được phương trình bậc nhất hai ẩn x và y.

Cách 2: Đặt ẩn phụ.

Cách 1:

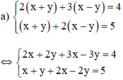
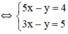 (hệ số của y bằng nhau nên ta trừ từng vế hai phương trình)

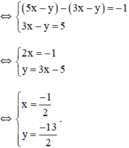
Vậy hệ phương trình có nghiệm duy nhất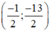 

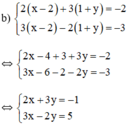
(Nhân hai vế pt 1 với 2; pt 2 với 3 để hệ số của y đối nhau)

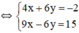 (Hệ số của y đối nhau nên ta cộng từng vế của hai pt)

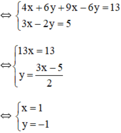
Vậy hệ phương trình có nghiệm duy nhất (1; -1).

Cách 2:

a) Đặt x + y = u và x – y = v (*)

Khi đó hệ phương trình trở thành

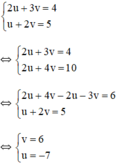
Thay u = -7 và v = 6 vào (*) ta được hệ phương trình:

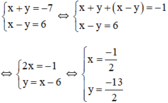
Vậy hệ phương trình có nghiệm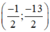 

b) Đặt x – 2 = u và y + 1 = v.

Khi đó hệ phương trình trở thành :

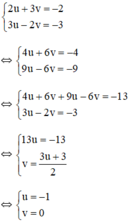
+ u = -1 ⇒ x – 2 = -1 ⇒ x = 1.

+ v = 0 ⇒ y + 1 = 0 ⇒ y = -1.

Vậy hệ phương trình có nghiệm (1; -1).

x - y = 3 3 x - 4 y = 2

Từ (1) rút ra được y = x – 3

Thế vào phương trình (2) ta được:

3x – 4.(x – 3) = 2 ⇔ 3x – 4x + 12 = 2 ⇔ x = 10

Từ x = 10 ⇒ y = x – 3 = 7.

Vậy hệ phương trình có nghiệm duy nhất (10 ; 7).

1.   3x( x - 2 ) - ( x - 2 ) = 0

<=> ( x-2).(3x-1)  = 0 => x = 2 hoặc x = \(\dfrac{1}{3}\)

2.    x( x-1 ) ( x² + x + 1 ) - 4( x - 1 )

<=> ( x - 1 ).( x (x^2 + x + 1 ) - 4 ) = 0

(phần này tui giải được x = 1 thôi còn bên kia giải ko ra nha )

3 \(\left\{{}\begin{matrix}\sqrt{5}x-2y=7\\\sqrt{5}x-5y=10\end{matrix}\right.\)<=> \(\left\{{}\begin{matrix}y=-1\\x=\sqrt{5}\end{matrix}\right.\)

\(1. 3x^2 - 7x +2=0\)

=>\(Δ=(-7)^2 - 4.3.2\)

        \(= 49-24 = 25\)

Vì 25>0 suy ra phương trình có 2 nghiệm phân biệt:

\(x_1\)=\(\dfrac{-\left(-7\right)+\sqrt{25}}{2.3}=\dfrac{7+5}{6}=2\)

\(x_2\)=\(\dfrac{-\left(-7\right)-\sqrt{25}}{2.3}=\dfrac{7-5}{6}=\dfrac{1}{3}\)