Cho vectơ a→ ≠ 0→. Xác định độ dài và hướng của vectơ a→ + a→.

Những câu hỏi liên quan
Cho vectơ \(\overrightarrow a \). Hãy xác định độ dài và hướng của hai vectơ \(\overrightarrow a + \overrightarrow a ,\left( { - \overrightarrow a } \right) + \left( { - \overrightarrow a } \right)\): (Hình 1)
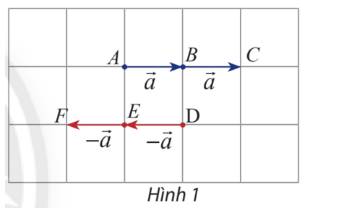
Dựa vào hình 1 ta thấy
Vectơ \(\overrightarrow a + \overrightarrow a = \overrightarrow {AC} \) có độ dài bằng 2 lần vectơ \(\overrightarrow a \)và cùng hướng với vectơ \(\overrightarrow a \)
Vectơ \(\left( { - \overrightarrow a } \right) + \left( { - \overrightarrow a } \right)= \overrightarrow {DF}\) có độ dài bằng 2 lần vectơ \(\left( { - \overrightarrow a } \right)\) và cùng hướng với vectơ \(\left( { - \overrightarrow a } \right)\)
Đúng 0
Bình luận (0)
Cho |a→ + b→| = 0. So sánh độ dài, phương và hướng của hai vectơ a→ và b→.
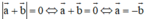
⇔ a→ và b→ là hai vec tơ đối nhau
⇔ a→ và b→ cùng phương, ngược hướng và có cùng độ dài.
Đúng 0
Bình luận (0)
Tích có hướng của hai vectơ
a
→
a
1
;
a
2
;
a
3
,
b
→
b
1
;
b
2...
Đọc tiếp
Tích có hướng của hai vectơ a → = a 1 ; a 2 ; a 3 , b → = b 1 ; b 2 ; b 3 là một vectơ, kí hiệu a → ; b → , được xác định bằng tọa độ:
A. a 2 b 2 - a 3 b 3 ; a 3 b 3 - a 1 b 1 ; a 1 b 1 - a 2 b 2
B. a 2 b 3 - a 3 b 2 ; a 3 b 1 - a 1 b 3 ; a 1 b 2 - a 2 b 1
C. a 2 b 3 + a 3 b 2 ; a 3 b 1 + a 1 b 3 ; a 1 b 2 + a 2 b 1
D. a 2 b 3 - a 3 b 2 ; a 3 b 1 + a 1 b 3 ; a 1 b 2 - a 2 b 1
a 2 b 3 - a 3 b 2 ; a 3 b 1 - a 1 b 3 ; a 1 b 2 - a 2 b 1
Đáp án B
Đúng 0
Bình luận (0)
Bài 1 : Cho tam giác ABC đều cạnh a. Gọi M là trung điểm của BC. Xác định và tính theo a độ dài vectơ BM + vectơ BA
Gọi O là trung điểm của AM
BM=BC/2=a/2
\(\Leftrightarrow AM=\dfrac{a\sqrt{3}}{2}\)
\(\Leftrightarrow MO=\dfrac{a\sqrt{3}}{4}\)
Xét ΔOMB vuông tại M có
\(BO^2=OM^2+BM^2\)
\(=a^2\cdot\dfrac{3}{16}+a^2\cdot\dfrac{1}{4}=a^2\cdot\dfrac{7}{16}\)
\(\Leftrightarrow BO=\dfrac{a\sqrt{7}}{4}\)
Xét ΔBMA có BO là đường trung tuyến
nên \(\overrightarrow{BM}+\overrightarrow{BA}=2\cdot\overrightarrow{BO}\)
\(\Leftrightarrow\left|\overrightarrow{BM}+\overrightarrow{BA}\right|=\dfrac{a\sqrt{7}}{2}\)
Đúng 0
Bình luận (0)
Cho A(1;3) B(-2;5) C(-4;0) a, Tính tọa độ vectơ AB,vectơ AC,vectơ BC,vectơ CB b, tính tích vô hướng của vectơ AB.vectơ CB,vectơ AC.vectơ BC c, tính độ dài đoạn thẳng AB,BC d,tính góc giữa 2 vectơ AB và AC e,tính tọa độ vectơ AB+ 2vectơCB
Cho \(\left| {\overrightarrow a + \overrightarrow b } \right| = 0\). So sánh độ dài, phương và hướng của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \).
\(\left| {\overrightarrow a + \overrightarrow b } \right| = 0 \Leftrightarrow \overrightarrow a + \overrightarrow b = \overrightarrow 0 \Leftrightarrow \overrightarrow a = - \overrightarrow b \)
\(\overrightarrow a = - \overrightarrow b \) suy ra hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là hai vecto đối nhau nên chúng cùng phương, ngược hướng và có độ dài bằng nhau.
Đúng 0
Bình luận (0)
Cho các véctơ
a
→
;
b
→
có độ dài bằng 1 và góc tạo bởi hai vectơ bằng 600. Xác định cosin góc giữa hai vectơ
u
→
a
→
+
2
b
→
;
v
→
a
→...
Đọc tiếp
Cho các véctơ a → ; b → có độ dài bằng 1 và góc tạo bởi hai vectơ bằng 600. Xác định cosin góc giữa hai vectơ u → = a → + 2 b → ; v → = a → - b →
A. -1/2
B. -1/4
C. -1/6
D. 0
Chọn C.
Ta có:
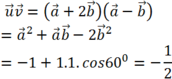
Mặt khác : ![]() nên
nên ![]()
![]() nên
nên ![]()
Suy ra ![]()
Đúng 0
Bình luận (0)
Cho hai vectơ a và b đều khác vectơ 0. Các khẳng định sau đúng hay sai?a, Hai vecto cùng hướng thì cùng phương.b, Hai vecto b→ và kb→ cùng phương.c, Hai vecto a→ và (-2)a→ cùng hướng.d) Hai vector ngược hướng với vector thứ ba khác vectơ 0→ thì cùng phương.
Đọc tiếp
Cho hai vectơ a và b đều khác vectơ 0. Các khẳng định sau đúng hay sai?
a, Hai vecto cùng hướng thì cùng phương.
b, Hai vecto b→ và kb→ cùng phương.
c, Hai vecto a→ và (-2)a→ cùng hướng.
d) Hai vector ngược hướng với vector thứ ba khác vectơ 0→ thì cùng phương.
TL: A, B, D: Đúng; C: Sai
Cho vectơ
a
→
có
a
→
2
. Tìm số thực x sao cho vectơ
x
a
→
có độ dài bằng 1 và cùng hướng với
a
→
A. x 1 B. x 2 C.
x
1
2
D.
x
-
1
2
Đọc tiếp
Cho vectơ a → có a → = 2 . Tìm số thực x sao cho vectơ x a → có độ dài bằng 1 và cùng hướng với a →
A. x = 1
B. x = 2
C. x = 1 2
D. x = - 1 2










