Cho bất phương trình x − 1 3 + mx ≤ m − 9 . Tìm x để bất phương trình có nghiệm x = 10 .

Những câu hỏi liên quan
1.Cho \(f\left(x\right)=mx^2+\left(4m-3\right)x+4m-6\). Tìm m để bất phương trình \(f\left(x\right)\ge0\) đúng với \(\forall x\in\left(-1;2\right)\)
2. Cho bất phương trình \(x^2-4x+2|x-3|-m< 0\). Tìm m để bất phương trình đã cho đúng với \(\forall x\in\left[1;4\right]\)
Cho bất phương trình 2 m 2 x + 10 − mx < 4 . Tìm m để bất phương trình có nghiệm x = − 3 .
Tìm m để hệ bất phương trình vô nghiệm \(\left\{{}\begin{matrix}mx\le m-3\\\left(m+3\right)x\ge m-9\end{matrix}\right.\)
Tìm m để bất phương trình \(\dfrac{x+1}{mx^2-4x+m-3}< 1\) có tập nghiệm là R
\(\Leftrightarrow\dfrac{mx^2-5x+m-4}{mx^2-4x+m-3}>0\)
BPT đã cho có tập nghiệm là R khi và chỉ khi:
\(\left\{{}\begin{matrix}\Delta_1=25-4m\left(m-4\right)< 0\\\Delta'_2=4-m\left(m-3\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-4m^2+16m+25< 0\\-m^2+3m+4< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m< \dfrac{4-\sqrt{41}}{2}\\m>\dfrac{4+\sqrt{41}}{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Bất phương trình mx\(^2\)+2(m+3)x+m+1\(\ge\)0 vô nghiệm khi và chỉ khi
Bất phương trình mx -
x
-
3
≤
m có nghiệm khi:
A
.
m
≤
2
4
B
.
m
≥
0
C
.
m
2
4
D...
Đọc tiếp
Bất phương trình mx - x - 3 ≤ m có nghiệm khi:
A . m ≤ 2 4
B . m ≥ 0
C . m < 2 4
D . m ≥ 2 4
Chọn A.
ĐK: x ≥ 3
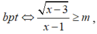
xét hs 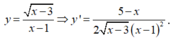
![]()
BBT:
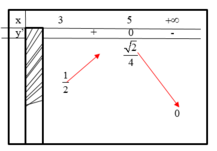
Vậy bất phương trình có nghiệm 
Đúng 0
Bình luận (0)
Bất phương trình
m
x
-
x
-
3
≤
m
có nghiệm khi: A.
m
≤
2
4
B.
m
≥
0
C.
m...
Đọc tiếp
Bất phương trình m x - x - 3 ≤ m có nghiệm khi:
A. m ≤ 2 4
B. m ≥ 0
C. m < 2 4
D. m ≥ 2 4
Tìm m để x = 2 là nghiệm bất phương trình: mx + 2 < x + 3 + m
A. m = 2
B. m < 3
C. m > 1
D. m < - 3
Do x = 2 là nghiệm của bất phương trình đã cho nên:
⇔ 2m + 2 < 2 + 3 + m
⇔ 2m – m < 2 + 3- 2
⇔ m < 3
Chọn đáp án B
Đúng 0
Bình luận (0)
xác định m để mỗi bất phương trình sau nghiệm đúng với mọi x
x^2 +mx -1 / 2x2 -2x +3
Xem chi tiết
Bạn dùng thanh này
để đánh rõ hơn nha :vvvv .
Đúng 1
Bình luận (0)












