Chọn A.
ĐK: x ≥ 3
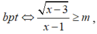
xét hs 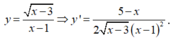
![]()
BBT:
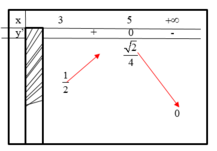
Vậy bất phương trình có nghiệm 
Chọn A.
ĐK: x ≥ 3
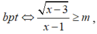
xét hs 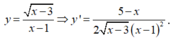
![]()
BBT:

Vậy bất phương trình có nghiệm 
Cho bất phương trình m . 3 x + 1 + ( 3 m + 2 ) ( 4 - 7 ) x + ( 4 + 7 ) x > 0
với m là tham số. Tìm tất cả các giá trị của tham số m để bất phương trình đã cho nghiệm đúng với mọi x ∈ ( - ∞ , 0 )
A. m > 2 + 2 3 3
B. m > 2 - 2 3 3
C. m ≥ 2 - 2 3 3
D. m ≥ - 2 - 2 3 3
Cho phương trình m . l n 2 ( x + 1 ) - ( x + 2 - m ) l n ( x + 1 ) - x - 2 = 0 (1). Tập hợp tất cả các giá trị của tham số m để phương trình (1) có hai nghiệm phân biệt thoả mãn 0 < x 1 < 2 < 4 < x 2 là khoảng . Khi đó a thuộc khoảng
![]()
![]()
![]()
![]()
Hàm số y = x 3 + (m + 3) x 2 + mx - 2 đạt cực tiểu tại x = 1 khi:
A. m = 1 B. m = 2
C. m = -3 D. m = 4
Hàm số y = x 3 + (m + 3) x 2 + mx - 2 đạt cực tiểu tại x = 1 khi:
A. m = 1 B. m = 2
C. m = -3 D. m = 4
Bất phương trình m x 2 - 2 ( m + 1 ) x + m + 7 < 0 vô nghiệm khi:
A . m ≥ 1 5
B . m > 1 4
C . m > 1 5
D . m > 1 25
Cho phương trình m - 1 log 1 2 2 x - 2 2 + 4 m - 5 log 1 2 1 ( x - 2 ) + 4 m - 4 = 0 (với m là tham số). Gọi S = a ; b là tập hợp các giá trị của m để phương trình có nghiệm trên đoạn 5 2 ; 4 . Tính a + b .
A. 7 3 .
B. - 2 3 .
C. - 3 .
D. 1034 237 .
Tìm các giá trị m ∈ ℝ để phương trình 5 x 2 + m x - 2 - 5 2 x 2 - m x - m + 2 = x - m x - m có nghiệm x ∈ 0 ; 1 .
A. - 1 ≤ m ≤ 0
B. 0 ≤ m ≤ 1 3
C. m ≤ - 1 hoặc m ≥ 0
D. - 3 ≤ m ≤ - 1
Bất phương trình lg2 – mlgx + m + 3 ≤ 0 có nghiệm x > 1 khi giá trị của m là:
A. - ∞ ; - 3 ∪ [ 6 ; + ∞ )
B. m < -3.
C. m > 6.
D. 3 < m < 6.
Cho phương trình sau:
m . log 1 2 2 x - 4 - 2 m 2 + 1 log 1 2 x - 4 + m 3 + m + 2 = 0
Tìm m để phương trình trên có 2 nghiệm phân biệt thỏa mãn 4 < x1 < x2 < 6 .
A. m ∈ 0 ; + ∞
B. m ∈ 0 ; + ∞ \ 1
C. m ∈ 0 ; + ∞ \ 2
D. m ∈ 0 ; + ∞ \ - 1