Cho tam giác ABC vuông tại A, AB = 6cm, góc B = α
Biết tg α = 5/12 . Hãy tính: Cạnh AC
Cho tam giác ABC vuông tại A, AB = 6cm, góc B = α
Biết tg α = 5/12 . Hãy tính: Cạnh BC
cho tam giác ABC vuông tại A. Biết AB=30cm góc B = α cot α\(\dfrac{5}{12}\) tính độ dài các cạnh BC, AC
Ta có: \(cot\alpha=\dfrac{5}{12}\)
\(\Rightarrow\dfrac{AC}{AB}=\dfrac{5}{12}\Leftrightarrow\dfrac{AC}{30}=\dfrac{5}{12}\)
\(\Rightarrow AC=\dfrac{5\cdot30}{12}=12,5\left(cm\right)\)
Ta có \(\Delta ABC\) vuông tại A áp dụng định lý Py-ta-go ta có:
\(BC=\sqrt{AC^2+AB^2}=\sqrt{30^2+12,5^2}=32,4\left(cm\right)\)
cho tam giác ABC vuông tại A , AB = 6cm , góc B=a
biết tga=5/12 , hãy tính
a) cạnh AC
b) cạnh bc
\(a,\tan\widehat{B}=\dfrac{AC}{AB}=\dfrac{5}{12}\Leftrightarrow AC=\dfrac{5}{12}\cdot6=2,5\left(cm\right)\\ b,BC=\sqrt{AC^2+AB^2}=\sqrt{2,5^2+6^2}=6,5\left(cm\right)\left(pytago\right)\)
a) Xét tam giác ABC vuông tại A:
\(AC=tan\alpha.AB=\dfrac{5}{12}.6=2,5\left(cm\right)\)
b) Áp dụng đ/lý Pytago trong tam giác ABC vuông tại A:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{2,5^2+6^2}=6,5\left(cm\right)\)
Cho tam giác ABC vuông tại A ,AB=6cm,góc B=a
Biết tga=\(\frac{5}{12}\)hãy tính:
a) Cạnh AC
b) Cạnh BC
a, theo đề ta có : \(\frac{AC}{AB}\) = \(\frac{5}{12}\)
=> AC= 6.5:12=2,5
b, ta có: BC= \(\sqrt{AC^2+AB^2}\) = \(\frac{13}{2}\)
Cho tam giác ABC vuông tại A. Biết AB = 30cm, sinB = α, tanα = 5 12 . Tính cạnh BC và AC
Trong không gian, cho tam giác ABC vuông tại A, AB=2a, AC=a. Gọi α là góc ở đỉnh của hình nón nhận được khi quay tam giác ABC xung quanh cạnh AB. Tính cosα
A. cos α = 1 5
B. cos α = 2 5
C. cos α = 3 5
D. cos α = 4 5
Cho tam giác ABC cân tại A, đường cao BH. Hãy tính góc A và các cạnh AB, BC, nếu biết BH = h, ∠ C = α
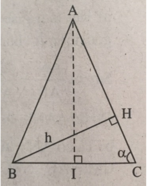
∠ A = 180 ° - 2 α . Tam giác vuông HBC có BC = h/sinα. Kẻ đường cao AI của tam giác ABC thì được
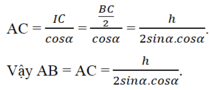
Cho tam giác ABC vuông tại A đặt AB= c; AC=b. Gọi M là điểm tùy ý trên cạnh BC sao cho góc MAB = α (0< α<90)
CM: AM=\(\frac{bc}{b.cos\text{ }\text{α}+c.sin\text{α}}\)
cho tam giác ABC vuông tại A ,ABC=60 độ;BD là Phân giác của ABC. ( D thuộc AC). Kẻ DE vuông góc BC ( E thuộc BC)
a. biết BC = 10cm AB=5 cm tính cạnh AC? b. so sánh: DE và DC
c chứng minh tg ABD = tg EBD
d chứng minh tg BDC cân
e kẻ CF vuông góc BD ( F thuộc tia BD) chứng minh BA;ED và CF đồng quy
GIÚP MIK VỚI Ạ MIK CẦN RẤT GẤP
a: \(AC=\sqrt{10^2-5^2}=5\sqrt{3}\left(cm\right)\)
b: ΔDEC vuông tại E
=>DE<DC
c: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
d: Xét ΔDBC có góc DBC=góc DCB
nên ΔDBC cân tại D
e: gọi giao của CF và AB là H
Xét ΔBHC có
BF,CA là đường cao
BF cắt CA tại D
=>D là trực tâm
=>HD vuông góc BC tại E
=>H,D,E thẳng hàng
=>BA,DE,CF là trực tâm