ctiếp tuyến ME và MF (E,F là tiếp điểm) sao cho góc E M O ^ = 30 0 . Biết chu vi ΔMEF là 30 cm
a, Tính độ dài dây EF
b, Tính diện tích ΔMEF
cho đường tròn tâm O và điểm A nằm ngoài đường tròn (O). Từ A kẻ đường thẳng (d) vuông góc với AO.M là điểm trên d, từ M kẻ hai tiếp tuyến ME và MF đến (O) E,F là hai tiếp điểm. MF cắt AE,AO thứ tự tại K và I
a) chứng minh năm điểm A,M,E,O,F cùng thuộc 1 đg tròn
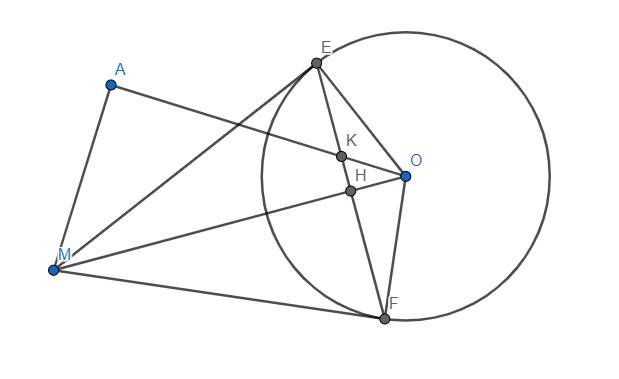
Đường tròn (O,R) và điểm M nằm ngoài đường tròn.Từ M kẻ tiếp tuyến ME với đường tròn (O), E là tiếp điểm . Đường thẳng qua E vuông góc OM tại H cắt đường tròn (O) tại điểm thứ hai là F
a, MF là tiếp tuyến
b, Đoạn MO cắt (O) tại I . Chứng minh I là tâm đường tròn nội tiếp tam giác MEF
c, Kẻ đường kính ED , FK vuông ED tại K . P là giao của MD và KF và Q là trung điểm FD . chứng minh H,P,Q thẳng hàng
Bài 8. Cho (O; R) và điểm M nằm ngoài đường tròn. Từ M kẻ tiếp tuyến ME với (O), E là tiếp điểm. Đường thẳng qua E vuông góc với OM tại H cắt (O) tại điểm thứ hai là F.
a) CMR: MF là tiếp tuyến của (O)
Giúp t với pls
a: Xét ΔOEF có
OH vừa là đường cao, vừa là trung tuyến
=>ΔOEF cân tại O
=>OE=OF và OH là phân giác của góc EOF
Xét ΔOEM và ΔOFM có
OE=OF
góc EOM=góc FOM
OM chung
=>ΔOEM=ΔOFM
=>góc OFM=90 độ
=>MF là tiếp tuyến của (O)
Cho (O,R) đường kính AB . Trên tiếp tuyến Ax của (O) lấy C. trên tiếp tuyến By của (O) lấy D sao cho AC+BD=CD ( C,D cùng nằm trên mặt phẳng bờ AB)
a) C/m CD tiếp xúc với (O)
b) Gọi M là tiếp điểm của CD và (O). Từ M kẻ MF vuông góc AB tại F, AD cắt MF ở I / C/m I là trung điểm của MF
c) Gọi E là điểm đối xứng của F qua M . C/m AD vuông góc BE
Cho đường tròn (O;R) và điểm A năm ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên đường thẳng d lấy điểm M khác điểm A. Qua điểm M vẽ hai tiếp tuyến ME và MF tới đường tròn (O) (E, F là tiếp điểm). EF cắt OM và OA lần lượt tại H và K
a, Chứng minh: H là trung điểm EF
b, Chứng minh: O,M,A,F cùng thuộc 1 đường tròn
c, Chứng minh:OK.OA = R2
d, Xác định vị trí điểm M trên đường thẳng d để tam giác OHK có diện tích lớn nhất
o l m . v n
(ko cần vẽ hình, giải chi tiết)
Cho đường tròn (O; R) và điểm A nằm ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên đường thẳng d lấy điểm M khác điểm A. Qua điểm M vẽ hai tiếp tuyến ME và MF tới đường tròn (O) (E và F là các tiếp điểm). EF cắt OM và OA lần lượt tại H và K.
1) Chứng minh: H là trung điểm của EF.
2) Chứng minh rằng bốn điểm O, M, A, F cùng thuộc một đường tròn.
3) Chứng minh: \(OK.OA=R^2\)
1: Xét (O) cso
ME,MF là tiếp tuyến
=>ME=MF
mà OE=OF
nên OM là trung trực của EF
=>OM vuông góc EF tại H và H là trung điểm của EF
2: Xét tứ giác OFAM có
góc OFM=góc OAM=90 độ
=>OFAM nội tiếp
3: Xét ΔOFK và ΔOAF có
góc OFK=góc OAF
góc FOK chung
Do đó: ΔOFK đồng dạng với ΔOAF
=>OF/OA=OK/OF
=>OK*OA=R^2
Cho đường tròn (O; R) đường kính BC và một điểm A nằm trên đường tròn sao
cho AB = R. Gọi H là trung điểm của dây cung AC.
a) Tính số đo các góc của tam giác ABC.
b) Qua C vẽ tiếp tuyến của đường tròn (O) cắt tia OH tại D. Chứng minh DA là tiếp
tuyến của đường tròn (O).
c) Tính độ dài bán kính của đường tròn ngoại tiếp tam giác ACD theo R.
d) Trên tia đối của tia AC lấy điểm M, từ M vẽ hai tiếp tuyến ME và MF với đường
tròn (O) tại E và F. Chứng minh ba điểm D, E, F thẳng hàng.
(ko cần vẽ hình, giải chi tiết)
Cho đường tròn (O; R) và điểm A nằm ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên đường thẳng d lấy điểm M khác điểm A. Qua điểm M vẽ hai tiếp tuyến ME và MF tới đường tròn (O) (E và F là các tiếp điểm). EF cắt OM và OA lần lượt tại H và K.
1) Chứng minh: H là trung điểm của EF.
2) Chứng minh rằng bốn điểm O, M, A, F cùng thuộc một đường tròn.
3) Chứng minh: \(OK.OA=R^2\)
a) Ta thấy \(OE=OF\Rightarrow\) O thuộc trung trực của EF.
Mặt khác, theo tính chất của 2 tiếp tuyến cắt nhau, \(ME=MF\), suy ra M cũng nằm trên trung trực của EF.
\(\Rightarrow\)OM là trung trực của EF. Mà OM cắt EF tại H nên H là trung điểm EF (đpcm)
b) Ta thấy \(\widehat{OAM}+\widehat{OFM}=90^o+90^o=180^o\) nên tứ giác OAMF nội tiếp hay 4 điểm O, M, A, F cùng thuộc 1 đường tròn.
c) Vì OM là trung trực EF nên \(OM\perp EF\) tại H \(\Rightarrow\widehat{MHK}=90^o\)
Từ đó dễ thấy tứ giác AMHK nội tiếp \(\Rightarrow OA.OK=OH.OM\)
Mà \(OH.OM=OE^2=R^2\) (hệ thức lượng trong tam giác vuông)
\(\Rightarrow OA.OK=R^2\) (đpcm)
Từ điểm M ở ngoài ( O;R ) vẽ tiếp tuyến MC và cát tuyến MAB sao cho điểm O không nằm ngoài goc BMC. MO cắt (O) tại E,F (ME<MF)Giả sử (O;R) không đổi, điểm M cố định, cát tuyến MAB quay quanh M. Hãy tìm GTLN của tống MA+MB