Cho biết
cos α + sin α cos α - sin α = 5
Tính tanα
Những câu hỏi liên quan
bài 1: a)biết sin α=√3/2.tính cos α,tan α,cot α
b)cho tan α=2.tính sin α,cos α,cot α
c)biết sin α=5/13.tính cos,tan,cot α
bài 2
biết sin α x cos α=12/25.tính sin,cos α
1:
a: sin a=căn 3/2
\(cosa=\sqrt{1-sin^2a}=\sqrt{1-\dfrac{3}{4}}=\sqrt{\dfrac{1}{4}}=\dfrac{1}{2}\)
\(tana=\dfrac{\sqrt{3}}{2}:\dfrac{1}{2}=\sqrt{3}\)
cot a=1/tan a=1/căn 3
b: \(tana=2\)
=>cot a=1/tan a=1/2
\(1+tan^2a=\dfrac{1}{cos^2a}\)
=>\(\dfrac{1}{cos^2a}=5\)
=>cos^2a=1/5
=>cosa=1/căn 5
\(sina=\sqrt{1-cos^2a}=\sqrt{\dfrac{4}{5}}=\dfrac{2}{\sqrt{5}}\)
c: \(cosa=\sqrt{1-\left(\dfrac{5}{13}\right)^2}=\dfrac{12}{13}\)
tan a=5/13:12/13=5/12
cot a=1:5/12=12/5
Đúng 0
Bình luận (0)
Tìm đẳng thức đúng:A. tg
α
sin
α
+ cos
α
B. tg
α
sin
α
- cos
α
C. tg
α
sin
α
. cos
α
D. tgα sin
α
/cos
α
Đọc tiếp
Tìm đẳng thức đúng:
A. tg α = sin α + cos α B. tg α = sin α - cos α
C. tg α = sin α . cos α D. tgα = sin α /cos α
Cho góc nhọn α. Biết sin α · cos α = 12 / 25 , tính sin α, cos α, tan α.
Ta có : P = sin3 α + cos3 α = ( sinα + cosα) 3 - 3sin α.cosα(sinα + cosα)
Ta có (sin α + cos α) 2 = sin2α + cos2α + 2sinα.cosα = 1 + 24/25 = 49/25.
Vì sin α + cosα > 0 nên ta chọn sinα + cosα = 7/5.
Thay 
vào P ta được 
Cho góc nhọn α biết rằng cos α - sin α = 1/3 . Giá trị của sin α .cos α là
A. 2 3
B. 3 2
C. 4 9
D. 9 4
Chứng minh các hệ thức:
a) \(\dfrac{cos\text{ α }}{1-sin\text{ α}}=\dfrac{1+sin\text{ α}}{cos\text{ α}}\)
b)\(\dfrac{\left(sin\text{ α }+cos\text{ α }\right)^2-\left(sin\text{ α }-cos\text{ α }\right)^2}{sin\text{ α }cos\text{ α }}=4\)
a: \(\dfrac{\cos\alpha}{1-\sin\alpha}=\dfrac{1+\sin\alpha}{\cos\alpha}\)
\(\Leftrightarrow\cos^2\alpha=1-\sin^2\alpha\)(đúng)
Đúng 0
Bình luận (0)
b: Ta có: \(\dfrac{\left(\sin\alpha+\cos\alpha\right)^2-\left(\sin\alpha-\cos\alpha\right)^2}{\sin\alpha\cdot\cos\alpha}\)
\(=\dfrac{4\cdot\sin\alpha\cdot\cos\alpha}{\sin\alpha\cdot\cos\alpha}\)
=4
Đúng 0
Bình luận (0)
28 tháng 7 2021 lúc 17:24
Cho sin α + cos α=√2
a, Tính cos α, sin α, tan α, cot α
b, Tính F = \(sin^5\alpha+cos^5\alpha\)
Chứng minh R sin4α + sin2α . cos2α + cos2α 1dfrac{sintext{α}}{1-costext{α}}+dfrac{sintext{α}}{1+costext{α}}+dfrac{2}{sintext{α}}dfrac{sintext{α}}{1+costext{α}}+dfrac{1+costext{α}}{sintext{α}}dfrac{2}{sintext{α}}
Đọc tiếp
Chứng minh R
sin4α + sin2α . cos2α + cos2α = 1
\(\dfrac{sin\text{α}}{1-cos\text{α}}\)+\(\dfrac{sin\text{α}}{1+cos\text{α}}\)+\(\dfrac{2}{sin\text{α}}\)
\(\dfrac{sin\text{α}}{1+cos\text{α}}\)+\(\dfrac{1+cos\text{α}}{sin\text{α}}\)=\(\dfrac{2}{sin\text{α}}\)
a: VT=sin^2a(sin^2a+cos^2a)+cos^2a
=sin^2a+cos^2a
=1=VP
b: \(VT=\dfrac{sina+sina\cdot cosa+sina-sina\cdot cosa}{1-cos^2a}=\dfrac{2sina}{sin^2a}=\dfrac{2}{sina}=VP\)
c: \(VT=\dfrac{sin^2a+1+2cosa+cos^2a}{sina\left(1+cosa\right)}\)
\(=\dfrac{2\left(cosa+1\right)}{sina\left(1+cosa\right)}=\dfrac{2}{sina}=VP\)
Đúng 1
Bình luận (0)
Tính:F=Cos(π/4+α) x cos(π/4-α)
G=Sin(π/3+α) x cos(π/3-α)
H=cos(π/2-α) x sin(π/2+α)
I=sin(π/4+α) - cos(π/4-α)
K=cos(π/6-x) - sin(π/3+x)
Cho góc
α
cho thỏa 0
α
π
4
và sin
α
+ cos
α
5
2
Tính P sin
α
-cos
α
.
Đọc tiếp
Cho góc α cho thỏa 0 < α < π 4 và sin α + cos α = 5 2 Tính P = sin α -cos α .
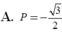
Cho biết 0≤α≤π20≤α≤π2 sao cho
sin3(α)+cos3(α)=1sin3(α)+cos3(α)=1
Và β=sin(α)+cos(α)β=sin(α)+cos(α)
a) Tính ∑α=07π2(sin−1(β)+α)∑α=07π2(sin−1(β)+α)
b) Chứng minh rằng số ββ thỏa đề bài là nghiệm của phương trình: β3−6β+5=0