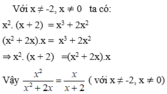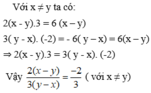\(\left(x+y\right)^2+\left(x-y\right)^2=2\left(x^2+y^2\right)\)

\(\Leftrightarrow x^2+2xy+y^2+x^2-2xy=2\left(x^2+y^2\right)\)

\(\Leftrightarrow2x^2+2y^2=2\left(x^2+y^2\right)\left(đúng\right)\)

Vậy đẳng thức đã được chứng minh

VT=(x+y)^2+(x-y)^2

=x^2+2xy+y^2+x^2-2xy+y^2

=2x^2+2y^2

=2(x^2+y^2)=VP

Vậy đẳng thức đã được chứng minh

BĐT này sai nha bạn.

Nó chỉ đúng khi \(x>0\)

Với \(x>0\) thì bất đẳng thức tương đương với \(x^2+1\ge2x\)

\(\Leftrightarrow x^2-2x+1\ge0\) \(\Leftrightarrow\left(x-1\right)^2\ge0\) (luôn đúng)

\(\Rightarrow\) Điều cần chứng minh là đúng

\(\dfrac{x^2+1}{x}=\dfrac{x^2}{x}+\dfrac{1}{x}=x+\dfrac{1}{x}\)

Theo bất đẳng thức Cô - si, ta có:

\(x+\dfrac{1}{x}\ge2\sqrt{x.\dfrac{1}{x}}=2\sqrt{1}=2\)

Vậy \(\dfrac{x^2+1}{x}\ge2\)

1 cách chứng minh khác (chứng minh tương đương)

\(\dfrac{x^2+1}{x}\ge2\\ \Leftrightarrow x^2+1\ge2x\\ \Leftrightarrow x^2-2x+1=\left(x-1\right)^2\ge0\left(\text{luôn đúng}\right)\)

Vậy BĐT ban đầu được chứng minh

\(\left(x-y\right)^3+4y\left(2x^2+y^2\right)=\left(x+y\right)^3+2y\left(x^2+y^2\right)\)

\(\Leftrightarrow x^3-3x^2y+3xy^2-y^3+8x^2y+4y^3=x^3+3x^2y+3xy^2+y^3+2x^2y+2y^3\)

\(\Leftrightarrow\left(-3x^2y+8x^2y\right)+3xy^2+3y^3=\left(3x^2y+2x^2y\right)+3xy^2+3y^2\)

\(\Leftrightarrow5x^2y+3xy^2+3y^2=5x^2y+3xy^2+3y^2\)

x^5- 1/ x-1= x^4+ x^3+ x^2+ x+ 1 

<=> x^5 - 1 = (x - 1)(x^4 + x^3 + x^2 + x + 1)

<=> x^5 - 1 = x^5 + x^4 + x^3  + x^2 + x - x^4 - x^3 - x^2 - x - 1

<=> x^5 - 1 = x^5 - 1 (đúng)

=> đpcm

a) Ta có:

\(VT=\left(a-b\right)^2\)

\(=a^2-2ab+b^2\)

\(=a^2+2ab+b^2-4ab\)

\(=\left(a+b\right)^2-4ab=VP\left(dpcm\right)\)

b) Ta có:

\(VT=\left(x+y\right)^2+\left(x-y\right)^2\)

\(=x^2+2xy+y^2+x^2-2xy+y^2\)

\(=\left(x^2+y^2\right)+\left(x^2+y^2\right)\)

\(=2\left(x^2+y^2\right)=VP\left(dpcm\right)\)