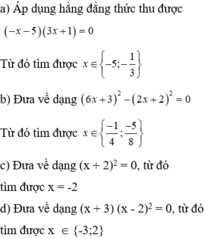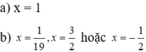\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)

\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)

\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)

\(\Leftrightarrow x^2-9-x^2+3x=0\)

\(\Leftrightarrow3x-9=0\)

\(\Leftrightarrow3x=9\)

\(\Leftrightarrow x=3\left(n\right)\)

Vậy \(S=\left\{3\right\}\)

\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)

\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)

\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)

\(\Leftrightarrow12x-9-12x+20+2x-7>0\)

\(\Leftrightarrow2x+4>0\)

\(\Leftrightarrow2x>-4\)

\(\Leftrightarrow x>-2\)

1. 4x-12=0

<=>4x=12

<=>x=3

2.  x.(x+1)-(x+2)(x+3)=7

<=>x²+x-x²-3x-2x-6=7

<=>x²-x²+x-2x-3x=7+6

<=>-4x=13

<=>x=\(-\dfrac{13}{4}\)

3.   7+2x=22-3x

<=>2x+3x=22-7

<=>5x=15

<=>x=3

4.  (x-1)-(2x-1)=9-x

<=>x-1-2x+1=9-x

<=>x-2x+x=9+1-1

<=>0x=9

vô nghiệm

1: Ta có: \(\dfrac{3}{x-3}+\dfrac{4}{x+3}=\dfrac{3x-7}{x^2-9}\)

\(\Leftrightarrow\dfrac{3x+9}{\left(x-3\right)\left(x+3\right)}+\dfrac{4x-12}{\left(x-3\right)\left(x+3\right)}=\dfrac{3x-7}{\left(x-3\right)\left(x+3\right)}\)

Suy ra: \(3x+9+4x-12=3x-7\)

\(\Leftrightarrow4x=-7+12-9=-4\)

hay \(x=-1\left(nhận\right)\)

2: Ta có: \(\dfrac{3}{x-4}-\dfrac{4}{x+4}=\dfrac{3x-4}{x^2-16}\)

\(\Leftrightarrow\dfrac{3x+12}{\left(x-4\right)\left(x+4\right)}-\dfrac{4x-16}{\left(x+4\right)\left(x-4\right)}=\dfrac{3x-4}{\left(x-4\right)\left(x+4\right)}\)

Suy ra: \(3x+12-4x+16=3x-4\)

\(\Leftrightarrow28-4x=-4\)

\(\Leftrightarrow4x=32\)

hay \(x=8\left(tm\right)\)

3: Ta có: \(\dfrac{5x^2-12}{x^2-1}+\dfrac{3}{x-1}=\dfrac{5x}{x+1}\)

Suy ra: \(5x^2-12+3x+3=5x^2-5x\)

\(\Leftrightarrow3x-9+5x=0\)

\(\Leftrightarrow8x=9\)

hay \(x=\dfrac{9}{8}\left(nhận\right)\)

Đề là \(...-x^3-x-12\) thì pt này không giải được

Phải là \(x^2\)

a)

\(9^{16-x}=27^{x+4}\\ \Leftrightarrow3^{2.\left(16-x\right)}=3^{3.\left(x+4\right)}\\ \Leftrightarrow2.\left(16-x\right)=3.\left(x+4\right)\\ \Leftrightarrow32-2x-3x-12=0\\ \Leftrightarrow-5x=-20\Leftrightarrow x=4\)

b)

\(16^{x-2}=0,25.2^{-x+4}\\ \Leftrightarrow2^{4\left(x-2\right)}=0,25.2^{-x+4}\\ \Leftrightarrow2^{4x-8+x-4}=0,25\\ \Leftrightarrow2^{5x-12}=0,25\Leftrightarrow5x-12=\log_20,25\\ \Leftrightarrow5x-12=-2\\ \Leftrightarrow x=2\)

a) ( 4x - 1 ) (x - 3) - ( x - 3 ) ( 5x + 2 ) = 0 

<=>  (x - 3)(4x - 1 - 5x - 2) = 0

<=>  (x - 3)(-x - 3) = 0

<=>  x  = 3 hoặc x = -3

b) ( x + 3 ) ( x - 5 ) + ( x + 3 ) ( 3x - 4) = 0 

<=>  (x + 3)(x - 5 + 3x - 4) = 0

<=>  (x + 3)(4x - 9) = 0

<=>  x = -3 hoặc x = 9/4

c) ( x + 6 ) ( 3x - 1 )+ x² - 36 = 0 

<=>  3x^2 + 17x - 6 + x^2 - 36 = 0

<=>  4x^2 + 17x - 42 = 0

<=>  4x^2 + 24x - 7x - 42 = 0

<=>  4x(x + 6) - 7(x + 6) = 0

<=>  (4x - 7)(x + 6) = 0

<=>  x = -6 hoặc x = 7/4

d) ( x + 4 ) ( 5x + 9 ) - x² + 16 = 0 

<=>  5x^2 + 29x + 36 - x^2 + 16 = 0

<=>  4x^2 + 29x + 52 = 0

<=>  4x^2 + 16x + 13x + 42 = 0

<=>  4x(x + 4) + 13(x + 4) = 0

<=>  (4x + 13)(x + 4) = 0

<=>  x = -13/4 và x = -4

a) \(x^2-4x+4=25\\ \Rightarrow\left(x-2\right)^2=25\\ \Rightarrow\left[{}\begin{matrix}x-2=-5\\x-2=5\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=-3\\x=7\end{matrix}\right.\)

b) \(\left(5-2x\right)^2-16=0\\ \Rightarrow\left(5-2x\right)^2=16\\ \Rightarrow\left[{}\begin{matrix}5-2x=-4\\5-2x=4\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=4,5\\0,5\end{matrix}\right.\)

c) \(\left(x-3\right)^3-\left(x-3\right)\left(x^2+3x+9\right)+9\left(x+1\right)^2=15\\ \Rightarrow\left(x-3\right)^3-\left(x-3\right)^3+9\left(x+1\right)^2=15\\ \Rightarrow9\left(x+1\right)^2=15\\ \Rightarrow\left(x+1\right)^2=\dfrac{5}{3}\\ \Rightarrow\left[{}\begin{matrix}x+1=-\sqrt{\dfrac{5}{3}}\\x+1=\sqrt{\dfrac{5}{3}}\end{matrix}\right.\)

   \(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{3+\sqrt{15}}{3}\\x=\dfrac{-3+\sqrt{15}}{3}\end{matrix}\right.\)

a)\(\Leftrightarrow\)\(x^2-4x-21=0\)

\(\Leftrightarrow\)\(x^2-7x+3x-21=0\)

\(\Leftrightarrow\)\(x(x-7)+3(x-7)=0\)

\(\Leftrightarrow\)\((x-7)(x+3)=0\)

\(\Leftrightarrow\)\(\left[\begin{array}{} x=7\\ x=-3 \end{array} \right.\)

b)\(\Leftrightarrow\)\((5-2x)^2-4^2=0\)

\(\Leftrightarrow\)\((5-2x-4)(5-2x+4)=0\)

\(\Leftrightarrow\)\((-2x+1)(-2x+9)=0\)

\(\Leftrightarrow\)\(\left[\begin{array}{} x=\dfrac{1}{2}\\ x=\dfrac{9}{2} \end{array} \right.\)

c)\((x-3)^3-(x-3)(x^2+3x+9)+9(x+1)^2=15\)

\(\Leftrightarrow\)\(x^3-9x^2+27x-27-x^3+27+9x^2+18x+9-15=0\)

\(\Leftrightarrow\)\(45x-6=0\)

\(\Leftrightarrow\)\(x=\dfrac{2}{15}\)