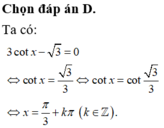Giải các phương trình sau 2tanx - 3cotx - 2 = 0

Những câu hỏi liên quan
Giải phương trình sau: 2tanx + 3cotx = 4
2tanx + 3cotx = 4.
Điều kiện: cosx ≠ 0 và sinx ≠ 0. Ta có
2 tan 2 x – 4 tan x + 3 = 0
Phương trình vô nghiệm đối với tanx, do đó phương trình đã cho vô nghiệm.
Đúng 0
Bình luận (0)
Giải các phương trình sau: 2 tan 2 x + 3 tan x + 2 c o t 2 x + 3 c o t x + 2 = 0
2 tan 2 x + 3 tan x + 2 c o t 2 x + 3 c o t x + 2 = 0


Đúng 0
Bình luận (0)
ssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssss
1) Giai phuong trinh:
a) 2tanx - 3cotx - 2 = 0
ĐK: \(x\ne\dfrac{k\pi}{2}\)
\(2tanx-3cotx-2=0\)
\(\Leftrightarrow2tanx-\dfrac{3}{tanx}-2=0\)
\(\Leftrightarrow2tan^2x-2tanx-3=0\)
\(\Leftrightarrow tanx=\dfrac{1\pm\sqrt{7}}{2}\)
\(\Leftrightarrow x=arctan\left(\dfrac{1\pm\sqrt{7}}{2}\right)+k\pi\)
Đúng 1
Bình luận (0)
Giải các phương trình sau tanx = 3cotx
tanx = 3cotx (Điều kiện cosx ≠ 0 và sinx ≠ 0)
Ta có:
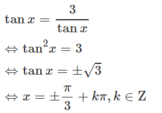
Đúng 0
Bình luận (0)
Tất cả các nghiệm của phương trình
tan
x
+
3
cot
x
−
3
−
1
0
là A.
x
π
4
+
k
π...
Đọc tiếp
Tất cả các nghiệm của phương trình tan x + 3 cot x − 3 − 1 = 0 là
A. x = π 4 + k π x = π 3 + k π k ∈ ℤ
B. x = − π 4 + k π x = π 6 + k π k ∈ ℤ
C. x = π 4 + k 2 π x = π 6 + k 2 π k ∈ ℤ
D. x = π 4 + k π x = π 6 + k π k ∈ ℤ
Đáp án A
P T ⇔ sin 2 x ≠ 0 tan x + 3 tan x − 3 − 1 = 0 ⇔ x ≠ k π 2 tan 2 x − 3 + 1 tan x + 3 = 0 ⇔ x ≠ k π 2 tan x = 3 tan x = 1
⇔ tan x = 3 tan x = 1 ⇔ x = π 3 + k π x = π 4 + k π k ∈ ℤ
Đúng 0
Bình luận (0)
Tìm tất cả các nghiệm của phương trình
tan
x
+
3
c
o
t
x
-
3
-
1
0
là A. hoặc
x
π
3
+
k
π
,
k
∈
Z
B.
x
-
π
4
+...
Đọc tiếp
Tìm tất cả các nghiệm của phương trình tan x + 3 c o t x - 3 - 1 = 0 là
A. hoặc x = π 3 + k π , k ∈ Z
B. x = - π 4 + k π hoặc x = π 6 + k π , k ∈ Z
C. x = π 4 + k 2 π hoặc x = π 6 + k 2 π , k ∈ Z
D. x = π 4 + k π hoặc x = π 6 + k π , k ∈ Z
giải phương trình lượng giác sau:
tanx-3cotx=4(sinx+\(\sqrt{3}\)cosx)
giải phương trình: \(\sqrt{3}\left(cosx+2tanx\right)+sinx=\frac{3}{cosx^2}\)
ĐKXĐ: ...
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}cosx+\dfrac{1}{2}sinx=\dfrac{3}{2}\left(1+tan^2x\right)-\sqrt{3}tanx\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{3}\right)=\dfrac{3}{2}\left(tanx-\dfrac{\sqrt{3}}{3}\right)^2+1\)
\(\left\{{}\begin{matrix}sin\left(x+\dfrac{\pi}{3}\right)\le1\\\dfrac{3}{2}\left(tanx-\dfrac{\sqrt{3}}{3}\right)^2+1\ge1\end{matrix}\right.\)
Đẳng thức xảy ra khi và chỉ khi: \(\left\{{}\begin{matrix}sin\left(x+\dfrac{\pi}{3}\right)=1\\tanx=\dfrac{\sqrt{3}}{3}\end{matrix}\right.\)
\(\Rightarrow x=\dfrac{\pi}{6}+k2\pi\)
Đúng 3
Bình luận (2)
Phương trình
3
c
o
t
x
-
3
0
có nghiệm là A.
x
π
3
+
k
2
π
k
∈
Z
B.
x
π
6
+
k
π
k...
Đọc tiếp
Phương trình 3 c o t x - 3 = 0 có nghiệm là
A. x = π 3 + k 2 π k ∈ Z
B. x = π 6 + k π k ∈ Z
C. x = π 3 + k 2 π hoặc x = - π 3 + k 2 π k ∈ Z
D. x = π 3 + k π k ∈ Z