Giải phương trình cos3x.tan4x = sin5x
A. x = k 2 π 3 , x = π 16 + k π 8 ( k ∈ Z )
B. x = k π , x = π 16 + k π 8 ( k ∈ Z )
C. x = k 2 π , x = π 16 + k 3 π 8 ( k ∈ Z )
D. x = k π 2 , x = π 16 + k 3 π 8 ( k ∈ Z )
Giải phương trình cos3x.tan4x = sin5x
A. 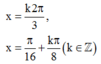
B. 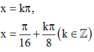
C. 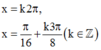
D. 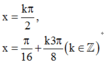
Đáp án B
Phương pháp giải: Quy đồng, đưa về dạng tích và sử dụng công thức tích thành tổng
Lời giải:
Điều kiện: ![]()
Ta có: 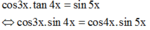
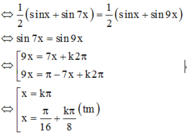
giải các phương trình sau
a) \(sin5x=sinx\)
b) \(cos\left(x+\dfrac{\pi}{3}\right)=-\dfrac{1}{2}\)
a: sin 5x=sin x
=>\(\left[{}\begin{matrix}5x=x+k2\Omega\\5x=\Omega-x+k2\Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4x=k2\Omega\\6x=\Omega+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{k\Omega}{2}\\x=\dfrac{\Omega}{6}+\dfrac{k\Omega}{3}\end{matrix}\right.\)
b; \(cos\left(x+\dfrac{\Omega}{3}\right)=-\dfrac{1}{2}\)
=>\(\left[{}\begin{matrix}x+\dfrac{\Omega}{3}=\dfrac{2}{3}\Omega+k2\Omega\\x+\dfrac{\Omega}{3}=-\dfrac{2}{3}\Omega+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{1}{3}\Omega+k2\Omega\\x=-\Omega+k2\Omega\end{matrix}\right.\)
Giải phương trình \(\dfrac{Sin5x}{5Sinx}=1\)
<=> sin5x=5sinx
<=> Sin5x-sinx=4sinx
<=> 2cos3x.sin2x=4sinx
<=>4cos3x.sinx.cosx=4sinx
<=>(cos3x.cosx-1).sinx=0
Sinx=0 hoặc cos3x.cosx -1=0
TH1. Sinx=0 => x=kπ
TH2: cos3x.cosx-1=0
<=> Cos3x.cosx=1
<=>cos4x + cos2x =2
<=> 2cos ²2x -1 +cos2x -2=0
<=> 2cos ²2x +cos 2x -3=0
Cos 2x= 1 =>. X=kπ/2
Cos2x= -3/2 <-1(loai)
Vậy x=kπ/2
ĐK: \(x\ne k\pi\)
\(\dfrac{sin5x}{5sinx}=1\)
\(\Leftrightarrow sin5x=5sinx\)
\(\Leftrightarrow sin5x-sinx=4sinx\)
\(\Leftrightarrow2cos3x.sin2x=4sinx\)
\(\Leftrightarrow4sinx.cosx.cos3x=4sinx\)
\(\Leftrightarrow cosx.cos3x=1\) (Vì \(sinx\ne0\))
\(\Leftrightarrow\dfrac{1}{2}\left(cos4x+cos2x\right)=1\)
\(\Leftrightarrow2cos^22x-1+cos2x=2\)
\(\Leftrightarrow2cos^22x+cos2x-3=0\)
\(\Leftrightarrow\left(cos2x-1\right)\left(2cos2x+3\right)=0\)
\(\Leftrightarrow cos2x=1\) (Vì \(2cos2x+3>0\))
\(\Leftrightarrow x=k\pi\left(l\right)\)
Vậy phương trình đã cho vô nghiệm
Giải các phương trình sau: cosx.tan3x = sin5x
cosx.tan3x = sin5x
Điều kiện: cos3x ≠ 0. Khi đó,
(3)⇔ cosx.sin3x = cos3x.sin5x
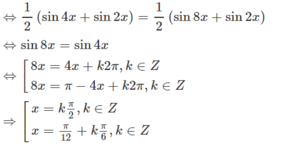
Kết hợp với điều kiện ta được nghiệm của phương trình là:
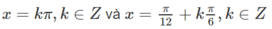
Giải phương trình: 4sin3x + sin5x - 2sinxcos2x = 0
4sin3x + sin5x – 2sinx.cos2x = 0
⇔ 4sin3x + sin5x – sin3x + sinx = 0
⇔ 3sin3x + sin5x + sinx = 0
⇔ 3sin3x + 2sin3x.cos2x = 0
⇔ sin3x(3 + 2cos2x) = 0.
Đáp số: x = kπ/3, k ∈ Z.
Giải các phương trình sin3x + sin5x = 0
sin3x + sin5x = 0
⇔ 2sin4x. cosx = 0
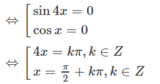
Vậy nghiệm của phương trình là:
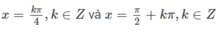
Giải phương trình: sin5x-sin3x=0
Giải các phương trình sau sin5x + cos5x = -1
Giải phương trình sau :
\(4\sin3x+\sin5x-2\sin x\cos2x=0\)
\(4\sin3x+\sin5x-2\sin x\cos2x=0\)
\(\Leftrightarrow\)\(4\sin3x+\sin5x-\sin3x+\sin x=0\)
\(\Leftrightarrow3\sin3x+\sin5x+\sin x=0\)
\(\Leftrightarrow3\sin3x+2\sin3x\cos2x=0\)
\(\Leftrightarrow\sin3x\left(3+2\cos2x\right)=0\)
Đáp số : \(x=k\dfrac{\pi}{3},k\in\mathbb{Z}\)