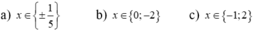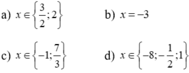Bài 2:

a: =>2x^2-4x+1=x^2+x+5

=>x^2-5x-4=0

=>\(x=\dfrac{5\pm\sqrt{41}}{2}\)

b: =>11x^2-14x-12=3x^2+4x-7

=>8x^2-18x-5=0

=>x=5/2 hoặc x=-1/4

a) BPT \(\Leftrightarrow-2\left(x^2-\dfrac{3}{2}x+\dfrac{7}{2}\right)>0\)

            \(\Leftrightarrow-2\left(x^2-2x\cdot\dfrac{3}{4}+\dfrac{9}{16}+\dfrac{47}{16}\right)>0\)

            \(\Leftrightarrow-\dfrac{47}{8}-2\left(x-\dfrac{3}{4}\right)^2>0\)  (Vô lý)

b) Bạn xem lại đề !

a) Do a = 3; c = -7 nên a và c trái dấu

Vậy phương trình luôn có hai nghiệm phân biệt

b) Theo Viét ta có:

x₁ + x₂ = -4/3

x₁x₂ = -7/3

Ta có:

2x₁ - (x₁ - x₂ - x₁x₂)

= 2x₁ - x₁ + x₂ + x₁x₂

= x₁ + x₂ + x₁x₂

= -4/3 - 7/3

= -11/3

\(3x^2+4x-7=0\)

\(a,\) Để pt có 2 nghiệm phân biệt thì \(\Delta>0\Rightarrow4^2-4.3.\left(-7\right)=100>0\)

Vậy pt có 2 nghiệm phân biệt \(x_1,x_2\)

\(b,\)Theo Vi-ét, ta có :

\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{4}{3}\\x_1x_2=\dfrac{c}{a}=-\dfrac{7}{3}\end{matrix}\right.\)

Ta có : \(2x_1-\left(x_1-x_2-x_1x_2\right)\)

\(=2x_1-x_1+x_2-x_1x_2\)

\(=x_1+x_2-x_1x_2\)

\(=-\dfrac{4}{3}-\left(-\dfrac{7}{3}\right)\)

\(=-\dfrac{4}{3}+\dfrac{7}{3}\)

\(=\dfrac{3}{3}=1\)

Vậy giá trị của biểu thức là \(1\)

3x² + 2x - 1 = 0

=> 3x² + 3x - x - 1 = 0

=> 3x(x + 1) - (x + 1) = 0

=> (3x - 1)(x + 1) = 0

=> \(\orbr{\begin{cases}3x-1=0\\x+1=0\end{cases}}\)

=> \(\orbr{\begin{cases}x=\frac{1}{3}\\x=-1\end{cases}}\)

x² - 5x + 6 = 0

=> x² - 2x - 3x + 6 = 0

=> x(x - 2) - 3(x - 2) = 0

=> (x - 3)(x - 2) = 0

=> \(\orbr{\begin{cases}x-3=0\\x-2=0\end{cases}}\)

=> \(\orbr{\begin{cases}x=3\\x=2\end{cases}}\)

3x² + 7x + 2 = 0

=> 3x² + 6x + x  + 2 = 0

=> 3x(x + 2) + (x + 2) = 0

=> (3x + 1)(x + 2) = 0

=> \(\orbr{\begin{cases}3x+1=0\\x+2=0\end{cases}}\)

=> \(\orbr{\begin{cases}x=-\frac{1}{3}\\x=-2\end{cases}}\)

1, \(3x^2+2x-1=0\Leftrightarrow3x^2+3x-x-1=0\)

\(\Leftrightarrow3x\left(x+1\right)-\left(x+1\right)=0\)

\(\Leftrightarrow\left(x+1\right)\left(3x-1\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\3x-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-1\\x=\frac{1}{3}\end{cases}}}\)

2, \(x^2-5x+6=0\Leftrightarrow x^2-2x-3x+6=0\)

\(\Leftrightarrow x\left(x-2\right)-3\left(x-2\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x-3\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\x-3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=2\\x=3\end{cases}}}\)

3, \(3x^2+7x+2=0\Leftrightarrow3x^2+6x+x+2=0\)

\(\Leftrightarrow3x\left(x+2\right)+\left(x+2\right)=0\)

\(\Leftrightarrow\left(x+2\right)\left(3x+1\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x+2=0\\3x+1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-2\\x=-\frac{1}{3}\end{cases}}}\)

\(x^2-4x+1=0\)

\(\Leftrightarrow\left(x^2-4x+4\right)=3\)

\(\Leftrightarrow\left(x-2\right)^2=3\)

\(\Leftrightarrow x=\sqrt{3}+2;x=2-\sqrt{3}\)

\(2x^2-6x+1=0\)

\(\Leftrightarrow4x^2-12x+2=0\)

\(\Leftrightarrow\left(2x-3\right)^2=7\)

\(\Leftrightarrow x=\frac{\sqrt{7}+3}{2};x=\frac{3-\sqrt{7}}{2}\)

\(3x^2+4x-4=0\)

\(\Leftrightarrow3x^2-2x+6x-4=0\)

\(\Leftrightarrow\left(x+2\right)\left(3x-2\right)=0\)

\(\Leftrightarrow x=-2;x=\frac{2}{3}\)

a) x = 4                 b) x = 3

c) x = 14               d) x = 1.

a: \(\Leftrightarrow\left(-x+3\right)\left(x+6\right)=18\)

\(\Leftrightarrow-x^2-6x+3x+18-18=0\)

\(\Leftrightarrow-x\left(x+3\right)=0\)

=>x=0 hoặc x=-3

b: \(\Leftrightarrow x\left(3x^2+6x-4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\3x^2+6x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2+2x-\dfrac{4}{3}=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\\left(x+1\right)^2=\dfrac{7}{3}\end{matrix}\right.\Leftrightarrow x\in\left\{0;\dfrac{\sqrt{21}}{3}-1;\dfrac{-\sqrt{21}}{3}-1\right\}\)

c: =>x(3x-5)=0

=>x=0 hoặc x=5/3

d: =>(x-2)(x+2)=0

=>x=2 hoặc x=-2

Điều kiện của phương trình là: 3 x 2   -   4 x   -   4   ≥   0 và 2x + 5 ≥ 0

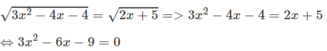
Phương trình cuối có hai nghiệm x 1   =   - 1 ,   x 2   =   3 . Cả hai giá trị này đều thỏa mãn các điều kiện và nghiệm đúng phương trình đã cho.

    Vậy phương trình đã có hai nghiệm  x 1   =   - 1 ,   x 2   =   3

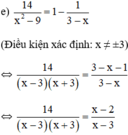
⇔ 14 = (x – 2)(x + 3)

⇔ 14 = x2 – 2x + 3x – 6

⇔ x2 + x – 20 = 0

Có a = 1; b = 1; c = -20

⇒ Δ = 12 – 4.1.(-20) = 81 > 0

Phương trình có hai nghiệm:

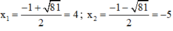
Cả hai nghiệm đều thỏa mãn điều kiện xác định.

Vậy phương trình có tập nghiệm S = {-5; 4}.