Cho đường tròn (C): x²+y²+2Ax+2By+C=0 và điểm M(x0;y0) . a) M nằm trong (C) khi nào? b) M nằm trên (C) khi nào? c) M nằm ngoài (C) khi nào?
Những câu hỏi liên quan
Cho đường tròn (C) : x2+ y2-2ax – 2by + c 0 (a2+ b2- c 0) . Hỏi mệnh đề nào sau đây sai? A. (C) có bán kính R
a
2
+
b
2
-
c
. B. (C) tiếp xúc với trục hoành khi và chỉ khi b2 R2. C. (C) tiếp xúc với trục tung khi và chỉ khi a R. ....
Đọc tiếp
Cho đường tròn (C) : x2+ y2-2ax – 2by + c= 0 (a2+ b2- c > 0) . Hỏi mệnh đề nào sau đây sai?
A. (C) có bán kính R= a 2 + b 2 - c .
B. (C) tiếp xúc với trục hoành khi và chỉ khi b2= R2.
C. (C) tiếp xúc với trục tung khi và chỉ khi a= R. .
D. (C) tiếp xúc với trục tung khi và chỉ khi b2= c.
Xét phương án C:
(C) tiếp xúc với trục Oy khi d ( I ; y ' O y ) = R ⇔ a = R .
Do đó đáp án (C) sai vì nếu a= -9 => R= -9 < 0 (vô lý)
Chọn C.
Đúng 0
Bình luận (0)
Cho phương trình x2+ y2-2ax- 2by+c 0 (1).Điều kiện để (1) là phương trình của đường tròn là A.a2+ b2- 4c 0. B. a2+ b2- c 0. C. a2+ b2- c2 0. D. a2+ b2- 2c 0.
Đọc tiếp
Cho phương trình x2+ y2-2ax- 2by+c= 0 (1).Điều kiện để (1) là phương trình của đường tròn là
A.a2+ b2- 4c> 0.
B. a2+ b2- c> 0.
C. a2+ b2- c2> 0.
D. a2+ b2- 2c> 0.
Đáp án B
Ta có: x2+ y2-2ax- 2by+c= 0
Tương đương: (x-a) 2+ ( y-b) 2= a2+ b2- c
Vậy điều kiện để (1) là phương trình đường tròn: a2+ b2 - c> 0.
Đúng 0
Bình luận (0)
Cho đường tròn (C) có phương trình
x
−
a
2
+
y
−
b
2
R
2
và điểm
M
(
x
0
;
y
0
)
nằm bên trong đường tròn. Đường thẳng ∆...
Đọc tiếp
Cho đường tròn (C) có phương trình x − a 2 + y − b 2 = R 2 và điểm M ( x 0 ; y 0 ) nằm bên trong đường tròn. Đường thẳng ∆ qua M cắt đường tròn tại hai điểm A, B sao cho M là trung điểm của AB. Phương trình của ∆ là:
A. ( a - x 0 ) ( x - x 0 ) + ( b - y 0 ) ( y - y 0 ) = 0
B. a + x 0 x − x 0 + b + y 0 y − y 0 = 0
C. ( a - x 0 ) ( x + x 0 ) + ( b - y 0 ) ( y + y 0 ) = 0
D. a + x 0 x + x 0 + b + y 0 y + y 0 = 0
Đáp án A.
Đường tròn (C) có tâm I(a;b).
Theo quan hệ vuông góc đường kính và dây cung: Nếu đường thẳng ∆ qua M cắt đường tròn tại hai điểm A, B sao cho M là trung điểm của AB thì ∆ ⊥ I M tại M.
Do đó, đường thẳng ∆: đi qua M x 0 ; y 0 và nhận M I → = a - x 0 ; b - y 0 làm VTPT.
Phương trình ∆: a - x 0 x - x 0 + b - y 0 y - y 0 = 0
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy,cho đường tròn (C) có phương trình (x-3)2+(y+1)2=10.Viết phương trình tiếp tuyến cua đường tròn đã cho tại điểm M∈(C),biết hoành độ của điểm M là X0=2
+
Gọi \(M\left(2;y_M\right)\) là tiếp điểm của (C):
\(\Leftrightarrow2^2+y_M^2-12+2y_M=0\)
\(\Leftrightarrow y_M^2+2y_M-8=0\)
\(\Leftrightarrow\left[{}\begin{matrix}y_M=2\\y_M=-4\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}M\left(2;2\right)\\M\left(2;-4\right)\end{matrix}\right.\)
* Với M(2;2)
Ta có: \(\overrightarrow{u}=\overrightarrow{IE}=\left(-1;3\right)\Rightarrow\overrightarrow{n}=\left(3;1\right)\)
\(\Rightarrow\left(D\right):3x+y-8=0\)
* Với M(2; -4)
Ta có: \(\overrightarrow{u}=\overrightarrow{IE}=\left(-1;-3\right)\Rightarrow\overrightarrow{n}=\left(-3;1\right)\)
\(\Rightarrow\left(D\right):-3x+y+4=0\)
Đúng 2
Bình luận (0)
Viết phương trình đường tròn (C): \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\) về dạng \({x^2} + {y^2} - 2{\rm{a}}x - 2by + c = 0\).
Ta có:
\(\begin{array}{l}{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\\ \Leftrightarrow {x^2} - 2ax + {a^2} + {y^2} - 2by + {b^2} - {R^2} = 0\\ \Leftrightarrow {x^2} + {y^2} - 2ax - 2by + c = 0\left( {{a^2} + {b^2} - {R^2} = c} \right)\end{array}\)
Đúng 0
Bình luận (0)
Cho hàm số
y
x
-
1
2
x
+
1
có đồ thị là (C). Gọi điểm M(x0; y0) với x0 -1 là điểm thuộc (C) biết tiếp tuyến của (C) tại điểm M cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A; B và tam giác OAB có trọng tâm G nằm trên đường t...
Đọc tiếp
Cho hàm số y = x - 1 2 x + 1 có đồ thị là (C). Gọi điểm M(x0; y0) với x0 > -1 là điểm thuộc (C) biết tiếp tuyến của (C) tại điểm M cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A; B và tam giác OAB có trọng tâm G nằm trên đường thẳng d: 4x+y=0. Hỏi giá trị của x0+2y0 bằng bao nhiêu?
A . -7/2
B. 7/2
C. 2
D.1
- Gọi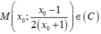 
với 
là điểm cần tìm.
- Gọi ∆ tiếp tuyến của (C) tại M ta có phương trình.
- Gọi 
- Khi đó ∆ tạo với hai trục tọa độ tam giác OAB có trọng tâm là
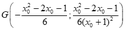
- Do G thuộc đường thẳng 4x+y=0 nên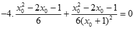 
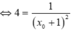(vì A; B không trùng O nên 
)
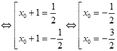
- Vì x0>-1 nên chỉ chọn 
Chọn A.
Đúng 0
Bình luận (0)
26 tháng 3 2023 lúc 22:10
trong mặt phẳng tọa độ Oxy cho điểm E(3;4), đường thẳng d : x + y - 1 0 và đường tròn (C) : x2 + y2 + 4x - 2y - 4 0 . Gọi M (m;1-m) là điểm nằm trên đường thẳng d và nằm ngoài đường tròn (C), từ M kẻ các tiếp tuyến MA, MB tới đường tròn (C), với A,B là các tiếp điểm. Gọi (E) là đường tròn tâm E và tiếp xúc với đường thẳng AB. Khi đường tròn (E) có chu vi lớn nhất. Tìm tọa độ điểm M
Đọc tiếp
trong mặt phẳng tọa độ Oxy cho điểm E(3;4), đường thẳng d : x + y - 1 = 0 và đường tròn (C) : x2 + y2 + 4x - 2y - 4 = 0 . Gọi M (m;1-m) là điểm nằm trên đường thẳng d và nằm ngoài đường tròn (C), từ M kẻ các tiếp tuyến MA, MB tới đường tròn (C), với A,B là các tiếp điểm. Gọi (E) là đường tròn tâm E và tiếp xúc với đường thẳng AB. Khi đường tròn (E) có chu vi lớn nhất. Tìm tọa độ điểm M
(C): x^2+y^2+4x-2y-4=0
=>(x+2)^2+(y-1)^2=9
=>I(-2;1); R=3
M thuộc d nên M(a;1-a)
M nằm ngoài (C) nên IM>R
=>IM^2>9
=>2a^2+4a-5>0
MA^2=MB^2=IM^2-IA^2=(a+2)^2+(-a)^2-9=2a^2+4a-5
=>x^2+y^2-2ax+2(a-1)y-6a+6=0(1)
A,B thuộc (C)
=>Tọa độ A,B thỏa mãn phương trình:
x^2+y^2+4x-2y-4=0(2)
(1)-(2)=(a+2)x-ay+3a-5=0(3)
Tọa độ A,B thỏa mãn (3) nên (3) chính là phương trình đường thẳng AB
(E) tiếp xúc AB nên (E): R1=d(E,AB)
Chu vi của (E) lớn nhất khi R1 lớn nhất
=>d(E;AB) lớn nhất
Gọi H là hình chiếu vuông góc của E lên AB
=>d(E,Δ)=EH<=EK=căn 10/2
Dấu = xảy ra khi H trùng K
=>AB vuông góc EK
vecto EK=(-1/2;3/2), AB có VTCP là (a;a+2)
AB vuông góc EK
=>-1/2a+3/2(a+2)=0
=>a=-3
=>M(-3;4)
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC nội tiếp đường tròn tâm I(2;1), tọng tâm
G
7
3
;
4
3
, phương trình đường thẳng AB: x-y+10. Giả sử điểm
C
(
x
0
;
y
0
)
, tính
2
x
0...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC nội tiếp đường tròn tâm I(2;1), tọng tâm G 7 3 ; 4 3 , phương trình đường thẳng AB: x-y+1=0. Giả sử điểm C ( x 0 ; y 0 ) , tính 2 x 0 + y 0
A. 18.
B. 10
C. 9.
D. 12
Cho 2 số nguyên dương a, b. CMR không tồn tại bộ 2 số (x, y) thỏa mãn đồng thời:
x^2 + 2ax - 2b = 0 và y^2 + 2by - 2a = 0
Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn
C
:
x
+
1
2
+
y
-
2
2
9
và điểm
I
-
3
;
3
. Đường thẳng...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn C : x + 1 2 + y - 2 2 = 9 và điểm I - 3 ; 3 . Đường thẳng ∆ : a x + b + c = 0 đi qua điểm I và cắt đường tròn (C) tại hai điểm A và B. Tiếp tuyến của A và B cắt nhau tại M. Biết điểm M thuộc đường thẳng x + 3 y - 4 = 0 . Tính P = 2 a + 3 b c
A. P = 1 3
B. P = - 11 4
C. P = 2 3
D. P = 1 4
Đáp án A.
Đường tròn (C) có tâm K(-1;2) và bán kính R = 3
Vậy phương trình đường thẳng D là
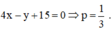
Đúng 0
Bình luận (0)