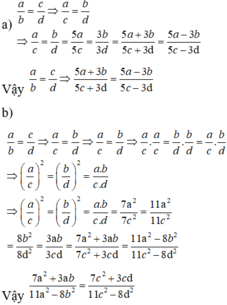3a2+5ab/7a2-10b2=3c2+5cd/7c2-10d2

Những câu hỏi liên quan
Cho a,b,c là các số dương thoả mãn √ a + √ b + √ c √ 2022P√3a2+2ab+3b2+√3b2+2bc+3c2+√3c2+2ca+3a2�3�2+2��+3�2+3�2+2��+3�2+3�2+2��+3�2
Đọc tiếp
Cho a,b,c là các số dương thoả mãn √ a + √ b + √ c = √ 2022
Chứng minh rằng: nếu
a
b
c
d
thì
a
)
5
a
+
3
b
5
a
−
3
b
5
c
+
3
d
5
c
−
3
d...
Đọc tiếp
Chứng minh rằng: nếu a b = c d thì
a ) 5 a + 3 b 5 a − 3 b = 5 c + 3 d 5 c − 3 d
b ) 7 a 2 + 3 a b 11 a 2 − 8 b 2 = 7 c 2 + 3 c d 11 c 2 − 8 d 2
Cho a/b=c/d. Chứng minh rằng : 3aa+5ab/3cc +5cd/7cc-10dd
Cho a/b=c/d. Chứng minh rằng : 3aa +5ab/7aa-10bb = 3cc+5cd/7cc-10dd
Chứng minh rằng nếu a,b,c > 0 thoả mãn a+b+c = 3 thì ab+a 3b2+10b+3 + bc+b 3c2+10c+3 + ca+c 3a2+10a+3 ≥
3 8
cho \(\frac{a}{b}=\frac{c}{d}\) . Cm \(\frac{7a^2+5ab}{7a^2-10b^2}=\frac{3c^2+5cd}{7c^2-10d}\)
Lời giải:
Đặt \(\frac{a}{b}=\frac{c}{d}=t\Rightarrow a=bt; c=dt\)
Khi đó :
\(\frac{3a^2+5ab}{7a^2-10b^2}=\frac{3(bt)^2+5.bt.b}{7(bt)^2-10b^2}=\frac{b^2(3t^2+5t)}{b^2(7t^2-10)}=\frac{3t^2+5t}{7t^2-10}\)
\(\frac{3c^2+5cd}{7c^2-10d^2}=\frac{3(dt)^2+5dt.d}{7(dt)^2-10d^2}=\frac{d^2(3t^2+5t)}{d^2(7t^2-10)}=\frac{3t^2+5t}{7t^2-10}\)
\(\Rightarrow \frac{3a^2+5ab}{7a^2-10b^2}=\frac{3c^2+5cd}{7c^2-10d^2}\) (đpcm)
Đúng 0
Bình luận (0)
Cho a/b = c/d với a, b, c, d > 0. Chứng minh rằng \(\dfrac{3a^2+10b^20-ab}{7a^2+b^2+5ab}=\dfrac{3c^2+10d^2-cd}{7c^2+d^2+5cd}\)
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
Sửa: \(\dfrac{3a^2+10b^2-ab}{7a^2+b^2+5ab}=\dfrac{3b^2k^2+10b^2-b^2k}{7b^2k^2+b^2+5b^2k}=\dfrac{b^2\left(3k^2+10-k\right)}{b^2\left(7k^2+1+5k\right)}=\dfrac{3k^2+10-k}{7k^2+1+5k}\left(1\right)\)
\(\dfrac{3c^2+10d^2-cd}{7c^2+d^2+5cd}=\dfrac{3d^2k^2+10d^2-d^2k}{7d^2k^2+d^2+5d^2k}=\dfrac{d^2\left(3k^2+10-k\right)}{d^2\left(7k^2+1+5k\right)}=\dfrac{3k^2+10-k}{7k^2+1+5k}\left(2\right)\)
\(\left(1\right)\left(2\right)\RightarrowĐpcm\)
Đúng 2
Bình luận (0)
\(Cho\frac{a}{b}=\frac{c}{d}.CM:\)\(\frac{2a^2-3ab+4b^2}{2b^2+5ab}=\frac{2c^2-3cd+4d^2}{2d^2+5cd}\)
cho tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\) chứng minh rằng:
\(\dfrac{3a^2+5ab}{7a^2-10b^2}=\dfrac{3c^2+5cd}{7c^2-10d^2}\)
Bạn tham khảo tại link sau:
Câu hỏi của Nguyễn Thanh Huyền - Toán lớp 7 | Học trực tuyến
Đúng 0
Bình luận (0)
cho tỉ lệ thức a phần b=c phần d.Chứng minh rằng 3a2+5ab phần 7a2-10b2 = 3c2+5cd phần 7c2-10d2