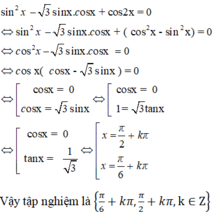\(\Leftrightarrow2-6sinx.cosx-2sinx+2cosx+2cos^2x=0\)

\(\Leftrightarrow3\left(1-2sinx.cosx\right)-2\left(sinx-cosx\right)+cos^2x-sin^2x=0\)

\(\Leftrightarrow3\left(sinx-cosx\right)^2-2\left(sinx-cosx\right)-\left(sinx-cosx\right)\left(sinx+cosx\right)=0\)

\(\Leftrightarrow\left(sinx-cosx\right)\left(sinx-2cosx-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sinx-cosx=0\Leftrightarrow x=\frac{\pi}{4}+k\pi\\sinx-2cosx=1\left(1\right)\end{matrix}\right.\)

Xét (1) \(\Leftrightarrow\frac{1}{\sqrt{5}}sinx-\frac{2}{\sqrt{5}}cosx=\frac{1}{\sqrt{5}}\)

Đặt \(\frac{1}{\sqrt{5}}=cosa\) với \(a\in\left(0;\pi\right)\)

\(\Rightarrow sinx.cosa-cosx.sina=cosa\)

\(\Leftrightarrow sin\left(x-a\right)=sin\left(\frac{\pi}{2}-a\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}x-a=\frac{\pi}{2}-a+k2\pi\\x-a=a+\frac{\pi}{2}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k2\pi\\x=2a+\frac{\pi}{2}+k2\pi\end{matrix}\right.\)

b) \(2sin^2x-3sinxcosx+cos^2x=0\)

\(\Leftrightarrow2tan^2x-3tanx+1=0\left(cosx\ne0\Leftrightarrow x\ne\dfrac{\pi}{2}+k\pi\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}tanx=1\\tanx=\dfrac{1}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}tanx=tan\dfrac{\pi}{4}\\tanx=\dfrac{1}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=arctan\left(\dfrac{1}{2}\right)+k\pi\end{matrix}\right.\left(k\in Z\right)\)

\(y=2sin^2x+3sinx.cosx+cos^2x\)

\(=-\left(1-2sin^2x\right)+\dfrac{3}{2}sin2x+\dfrac{1}{2}\left(2cos^2x-1\right)+\dfrac{1}{2}\)

\(=-cos2x+\dfrac{3}{2}sin2x+\dfrac{1}{2}cos2x+\dfrac{1}{2}\)

\(=\dfrac{3}{2}sin2x-\dfrac{1}{2}cos2x+\dfrac{1}{2}\)

\(=\dfrac{\sqrt{10}}{2}\left(\dfrac{3}{\sqrt{10}}sin2x-\dfrac{1}{\sqrt{10}}cos2x\right)+\dfrac{1}{2}\)

\(=\dfrac{\sqrt{10}}{2}sin\left(2x-arccos\dfrac{3}{\sqrt{10}}\right)+\dfrac{1}{2}\)

Vì \(sin\left(2x-arccos\dfrac{3}{\sqrt{10}}\right)\in\left[-1;1\right]\)

\(\Rightarrow y=\dfrac{\sqrt{10}}{2}sin\left(2x-arccos\dfrac{3}{\sqrt{10}}\right)+\dfrac{1}{2}\in\left[-\dfrac{\sqrt{10}}{2}+\dfrac{1}{2};\dfrac{\sqrt{10}}{2}+\dfrac{1}{2}\right]\)

\(\Rightarrow y_{min}=-\dfrac{\sqrt{10}}{2}+\dfrac{1}{2}\Leftrightarrow sin\left(2x-arccos\dfrac{3}{\sqrt{10}}\right)=-1\Leftrightarrow...\)

\(y_{max}=\dfrac{\sqrt{10}}{2}+\dfrac{1}{2}\Leftrightarrow sin\left(2x-arccos\dfrac{3}{\sqrt{10}}\right)=1\Leftrightarrow...\)

\(\Leftrightarrow\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)+\frac{3}{2}sin2x-m+2=0\)

\(\Leftrightarrow1-3sin^2x.cos^2x+\frac{3}{2}sin2x-m+2=0\)

\(\Leftrightarrow1-\frac{3}{4}sin^22x+\frac{3}{2}sin2x-m+2=0\)

\(\Leftrightarrow-\frac{3}{4}sin^22x+\frac{3}{2}sin2x+3=m\)

Đặt \(sin2x=t\Rightarrow t\in\left[-1;1\right]\)

\(\Rightarrow-\frac{3}{4}t^2+\frac{3}{2}t+3=m\)

Xét \(f\left(t\right)=-\frac{3}{4}t^2+\frac{3}{2}t+3\) trên \(\left[-1;1\right]\)

\(-\frac{b}{2a}=1\) ; \(f\left(-1\right)=\frac{3}{4}\) ; \(f\left(1\right)=\frac{15}{4}\)

\(\Rightarrow\frac{3}{4}\le f\left(t\right)\le\frac{15}{4}\Rightarrow\frac{3}{4}\le m\le\frac{15}{4}\)

1/ \(pt\Leftrightarrow\left(3cos^2x-sin^2x\right)\left(cos^2x-sin^2x\right)=0\)

\(\Leftrightarrow\left(\dfrac{3}{2}\left(1+cos2x\right)-\dfrac{1}{2}\left(1-cos2x\right)\right)\left(\dfrac{1}{2}\left(1+cos2x\right)-\dfrac{1}{2}\left(1-cos2x\right)\right)=0\)

\(\Leftrightarrow\left(2cos2x+1\right)cos2x=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\cos2x=-\dfrac{1}{2}\end{matrix}\right.\)

2/ \(pt\Leftrightarrow\left(sinx-1\right)\left(sin^2x+sinx+6\right)=0\)

\(\Leftrightarrow sinx=1\)

3/ \(pt\Leftrightarrow\dfrac{1-cos2x}{2}-4sin2x+\dfrac{7}{2}\left(1+cos2x\right)=0\)

\(\Leftrightarrow3cos2x-4sin2x=-4\)

\(\Leftrightarrow5\left(\dfrac{3}{5}cos2x-\dfrac{4}{5}sin2x\right)=-4\)

\(\Leftrightarrow cos\left(2x+arccos\dfrac{3}{5}\right)=-\dfrac{4}{5}\)

4,5 giải tương tự câu 3

Phương trình tương đương:

⇔(2sin⁡x−1)(cos⁡x+sin⁡x+2)=0

⇔cos⁡x(2sin⁡x−1)+sin⁡x(2sin⁡x−1)+2(2sin⁡x−1)=012sin⁡x+cos⁡x=−2sin⁡x+cos⁡x=2.sin⁡(x+π4)∈[−2;2]⇒sin⁡x+cos⁡x>−2" role="presentation" style="border:0px; color:rgb(40, 40, 40); direction:ltr; display:inline-table; float:none; font-family:times new roman,times,serif; font-size:18.18px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; padding:1px 0px; position:relative; white-space:nowrap; word-wrap:normal" class="MathJax_CHTML mjx-chtml">sin⁡x+cos⁡x=2.sin⁡(x+π4)∈[−2;2]⇒sin⁡x+cos⁡x>−2" role="presentation" style="border:0px; color:rgb(40, 40, 40); direction:ltr; display:inline-table; float:none; font-family:times new roman,times,serif; font-size:18.18px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; padding:1px 0px; position:relative; white-space:nowrap; word-wrap:normal" class="MathJax_CHTML mjx-chtml">sin⁡x+cos⁡x=2.sin⁡(x+π4)∈[−2;2]⇒sin⁡x+cos⁡x>−2 Do đó:

1)⇔sinx=12⇒⎡⎢ ⎢⎣π

a/ \(y=sin2x+\left(\sqrt{3}+1\right)cos2x+sin^2x-cos^2x-1\)

\(=sin2x+\sqrt{3}cos2x-1=2sin\left(2x+\frac{\pi}{3}\right)-1\)

Do \(-1\le sin\left(2x+\frac{\pi}{3}\right)\le1\Rightarrow-3\le y\le1\)

b/ \(y=2sin^2x-2cos^2x-3sinx.cosx-1\)

\(=-2cos2x-\frac{3}{2}sin2x-1=-\frac{5}{2}\left(\frac{3}{5}sinx+\frac{4}{5}cosx\right)-1\)

\(=-\frac{5}{2}sin\left(x+a\right)-1\Rightarrow-\frac{7}{2}\le y\le\frac{3}{2}\)

c/ \(y=1-sin2x+2cos2x+\frac{3}{2}sin2x=\frac{1}{2}sin2x+2cos2x+1\)

\(=\frac{\sqrt{17}}{2}\left(\frac{1}{\sqrt{17}}sin2x+\frac{4}{\sqrt{17}}cos2x\right)+1=\frac{\sqrt{17}}{2}sin\left(2x+a\right)+1\)

\(\Rightarrow-\frac{\sqrt{17}}{2}+1\le y\le\frac{\sqrt{17}}{2}+1\)

Chọn C