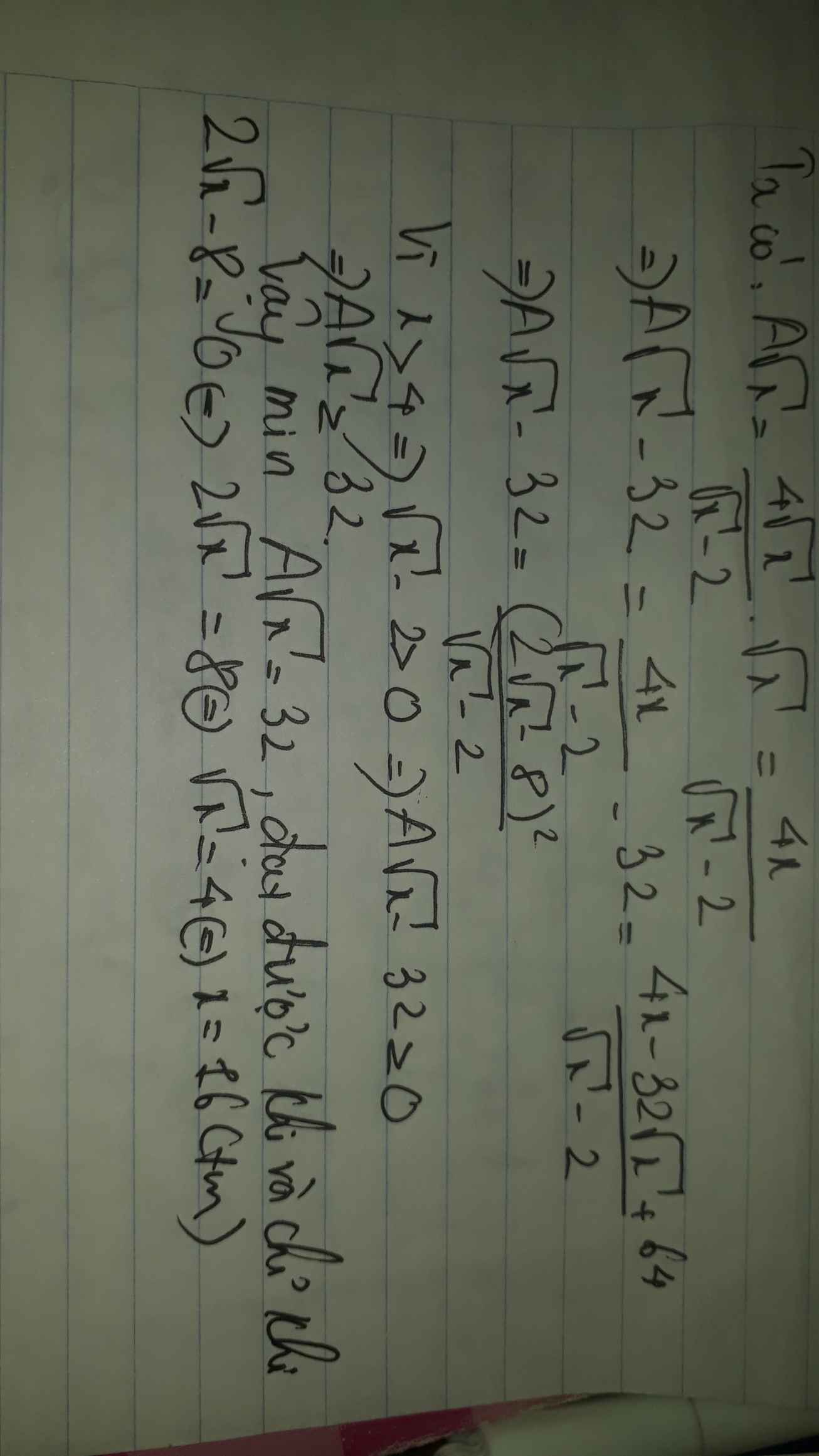Tìm giá trị nhỏ nhất của A = \(x-2\sqrt{x+2}\)

Những câu hỏi liên quan
Cho \(C=\left(\frac{\sqrt{x}+3}{\sqrt{x}-2}+\frac{\sqrt{x}+2}{3-\sqrt{x}}+\frac{\sqrt{x}+2}{x-5\sqrt{x}+6}\right):\left(1-\frac{\sqrt{x}}{\sqrt{x}+1}\right)\)
a) Rút gọn C
b)Tìm giá trị nguyên của x để C<0
c)với giá trị nào của x thì 1/C đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
Cho biểu thức
P=\(\dfrac{x\sqrt{x}+26\sqrt{x}-19}{x+2\sqrt{x}-3}-\dfrac{2\sqrt{x}}{\sqrt{x}-1}+\dfrac{\sqrt{x}-3}{\sqrt{x}+3}\)
a) Rút gọn biểu thức
b) Tìm giá trị của x khi p=4
c) tÌM GIÁ TRỊ NHỎ NHẤT CỦA P
d) Tính giá trị của P khi x=3-\(2\sqrt{2}\)
\(a,P=\dfrac{x\sqrt{x}+26\sqrt{x}-19-2x-6\sqrt{x}+x-4\sqrt{x}+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\left(x\ge0;x\ne1\right)\\ P=\dfrac{x\sqrt{x}-x+16\sqrt{x}-16}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}=\dfrac{\left(x+16\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\\ P=\dfrac{x+16}{\sqrt{x}+3}\\ b,P=4\Leftrightarrow\dfrac{x+16}{\sqrt{x}+3}=4\\ \Leftrightarrow x+16=4\sqrt{x}+12\\ \Leftrightarrow x-4\sqrt{x}+4=0\Leftrightarrow\left(\sqrt{x}-2\right)^2=0\\ \Leftrightarrow\sqrt{x}=2\Leftrightarrow x=4\left(tm\right)\)
\(c,P=\dfrac{x+16}{\sqrt{x}+3}=\dfrac{x-9+25}{\sqrt{x}+3}=\sqrt{x}-3+\dfrac{25}{\sqrt{x}+3}\\ P=\sqrt{x}+3+\dfrac{25}{\sqrt{x}+3}-6\ge2\sqrt{\left(\sqrt{x}+3\right)\cdot\dfrac{25}{\sqrt{x}+3}}-6=2\cdot5-6=4\\ P_{min}=4\Leftrightarrow\left(\sqrt{x}+3\right)^2=25\Leftrightarrow\sqrt{x}+3=5\left(\sqrt{x}+3>0\right)\\ \Leftrightarrow x=4\left(tm\right)\)
\(d,x=3-2\sqrt{2}\Leftrightarrow\sqrt{x}=\sqrt{2}-1\\ \Leftrightarrow P=\dfrac{3-2\sqrt{2}+16}{\sqrt{2}-1+3}=\dfrac{19-2\sqrt{2}}{\sqrt{2}+2}\\ P=\dfrac{\left(19-2\sqrt{2}\right)\left(2-\sqrt{2}\right)}{2}=\dfrac{42-23\sqrt{2}}{2}\)
Đúng 1
Bình luận (0)
tìm giá trị nhỏ nhất và giá trị lớn nhất của:
\(A=\sqrt{x+2}+\sqrt{2-x}\)
\(A^2=x+2+2\sqrt{\left(x+2\right)\left(2-x\right)}+2-x==4+2\sqrt{\left(x+2\right)\left(2-x\right)}\ge4\)
\(\Rightarrow A\ge2\).Nên GTNN của A là 2 đạt được khi \(\sqrt{\left(x+2\right)\left(2-x\right)}=0\Leftrightarrow\orbr{\begin{cases}x=-2\\x=2\end{cases}}\)
Áp dụng BĐT Bunhiacopxki ta có:
\(A^2=\left(\sqrt{x+2}+\sqrt{2-x}\right)^2\le\left(1^2+1^2\right)\left[\left(\sqrt{x+2}\right)^2+\left(\sqrt{2-x}\right)^2\right]\)
\(=2.\left(x+2+2-x\right)=2.4=8\)
\(\Rightarrow A\le\sqrt{8}\).Nên GTLN của A là \(\sqrt{8}\) đạt được khi \(\frac{\sqrt{x+2}}{1}=\frac{\sqrt{2-x}}{1}\Leftrightarrow\sqrt{x+2}=\sqrt{2-x}\)
\(\Rightarrow x+2=2-x\Leftrightarrow2x=0\Leftrightarrow x=0\)
Đúng 0
Bình luận (0)
bunhiacopxki là gì vậy ????????????????????
Đúng 0
Bình luận (0)
bunhiacopxki là j thế bạn Bảo Bình
Cho \(A=\sqrt{x}+\dfrac{2}{\sqrt{x}}\) Tìm tất cả giá trị của x để biểu thức A đạt giá trị nhỏ nhất
\(A=\sqrt{x}+\dfrac{2}{\sqrt{x}}\ge2\cdot\sqrt{\sqrt{x}\cdot\dfrac{2}{\sqrt{x}}}=2\sqrt{2}\)
Dấu '=' xảy ra khi \(\sqrt{x}\cdot\sqrt{x}=2\)
hay \(x=2\)
Đúng 0
Bình luận (0)
* Tìm giá trị nhỏ nhất của
A= \(x-2\sqrt{x+2}\)
`A=x-2sqrt{x+2}(x>=-2)`
`<=>A=x+2-2sqrt{x+2}+1-3`
`<=>A=(sqrt{x+2}-1)^2-3>=-3`
Dấu "=" xảy ra khi `sqrt{x+2}=1<=>x=-1(tmđk)`
Đúng 2
Bình luận (0)
Cho P= \(\dfrac{\sqrt{x}}{\sqrt{x}+2}+\dfrac{2}{\sqrt{x}-2}-\dfrac{4\sqrt{x}}{x-4}\)
a,Tìm điều kiện xác định và rút gọn P
b,Tìm x để P = \(\dfrac{2}{3}\)
c,Tìm x để P đạt giá trị nhỏ nhất . Tìm giá trị nhỏ nhất đó
a: ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne4\end{matrix}\right.\)
Ta có: \(P=\dfrac{\sqrt{x}}{\sqrt{x}+2}+\dfrac{2}{\sqrt{x}-2}-\dfrac{4\sqrt{x}}{x-4}\)
\(=\dfrac{x-2\sqrt{x}+2\sqrt{x}+4-4\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)
Đúng 0
Bình luận (0)
cho f(x)=1.32x2+\(\dfrac{3.1-2\sqrt{5}}{\sqrt{ }6.4-7.2}\)x +7.8 - 3.2
a. tình f(5-\(3\sqrt{2}\)
b. với giá trị nào của x thì f(x) đạt gia strij nhỏ nhất
tìm giá trị nhỏ nhất của f(x)
please ,mk cần gấp
A=\(\dfrac{4\sqrt{x}}{\sqrt{x}-2}\)với x>4 hãy tìm giá trị nhỏ nhất của \(A.\sqrt{x}\)
Cho biểu thức:
\(A=\left(1-\dfrac{\sqrt{x}}{\sqrt{x+1}}\right):\left(\dfrac{\sqrt{x}+3}{\sqrt{x}-2}+\dfrac{\sqrt{x}+2}{3-\sqrt{x}}+\dfrac{\sqrt{x}+2}{x-5\sqrt{x+6}}\right)\)
a) Rút gọn A
b) Tìm x để A<0
c) Tìm giá trị nhỏ nhất của A
d) Tính giá trị nguyên của x để A nhận giá trị nguyên