https://h.vn/hoi-dap/question/805552.html . Có lẽ tương tự

\(15x-49y=11\Leftrightarrow x=\frac{11+49y}{15}=\frac{11+4y+45y}{15}=\frac{11+4y}{15}+3y\)

x; y là nghiệm nguyên dương <=> \(\frac{11+4y}{15}\)nguyên dương 

<=> 11 + 4y chia hết cho 15 <=> 11 + 4y = 15t ( t là số tự nhiên ) 

<=> y = \(\frac{15t-11}{4}=\frac{16t-12-t+1}{4}=4t-3-\frac{t-1}{4}\)

=> t - 1 chia hết cho 4 

=> Đặt t - 1 = 4k => t = 4k + 1 (k là số tự nhiên)

=> y = 15k + 1 ; x = 49k + 4 

Vì x; y nhỏ nhất => Chọn k = 0 => x = 4; y = 1 là nghiệm cần tìm 

Lời giải:

\(15x-49y=11\Rightarrow 15x=49y+11\). Vì $x,y$ là các số nguyên nên:

\(\Rightarrow 49y+11\vdots 15\)

\(\Leftrightarrow 45y+4y+11\vdots 15\)

\(\Leftrightarrow 4y+11\vdots 15\Rightarrow 4y=15k-11\) (\(k\in\mathbb{Z}\) )

Lại có: \(15k-11=4y\vdots 4\)

\(\Leftrightarrow 16k-k-8-3\vdots 4\)

\(\Leftrightarrow -(k+3)\vdots 4\Leftrightarrow k+3\vdots 4\). Đặt \(k=4m-3(m\in\mathbb{Z}\) )

Khi đó: \(4y=15k-11=15(4m-3)-11=60m-56\)

\(\Rightarrow y=15m-14\)

Thay vào pt ban đầu: \(x=\frac{49y+11}{15}=\frac{49(15m-14)+11}{15}=49m-45\)

Vậy PT có nghiệm nguyên $(x,y)=(49m-45,15m-14)$ với $m\in\mathbb{Z}$

15x+49y=11

⇒15x=11-49y

⇒x=\(\dfrac{11-49y}{15}\)=\(\dfrac{15-45y-4-4y}{15}=1-3y-\dfrac{4\left(1+y\right)}{15}\). Do x,y nguyên ⇒\(\dfrac{11-49y}{15}\) là số nguyên⇔4(1+y)⋮15⇔1+y⋮15

Đặt 1+y=15K⇒y=15K-1. (K∈Z)

⇒x=1-45K+3-4K=4-49K

Vậy x=4-49K, y=15K-1

có thấy j đâu

Tìm nghiệm nguyên dương nhỏ nhất của pt: x²-15y²=1 đây nha giúp mk với

Đáp án A

Ta có  2 x . 15 x + 1 = 3 x + 3 ⇔ 2 x . 5 x + 1 = 3 2 ⇔ log 2 x . 5 x + 1 = log 3 2 ⇔ x log 2 + x + 1 log 5 = 2 log 3  

⇔ x log 2 + log 5 = 2 log 3 - log 5 ⇔ x = 2 log 3 - log 5 log 2 + log 5 = 2 log 3 - log 5 ⇒ a = 3 b = 5 .

Vậy S = 4009.

Chọn C

Ta có

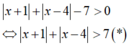
Bảng xét dấu

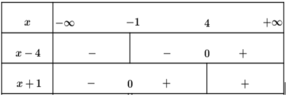
+ Trường hợp x ≤ - 1,(8) trở thành: -x-1-x+ 4 > 7  hay x < -4

So với trường hợp đang xét ta có tập nghiệm S₁ = (- ∞,-4)

+ Trường hợp  -1 < x  ≤4,

( *) trở thành: x+1-x+4> 7 

hay 5> 7 (vô lý)

Do đó, tập nghiệm 

+ Trường hợp x > 4

(*) trở thành: x+ 1+ x-4> 7 hay x> 5

So với trường hợp đang xét ta có tập nghiệm S₃ = (5, +∞)

Vậy 

Do đó;  x= 6 thỏa YCBT

12 hoặc - 12

Tick nhé bạn !!!