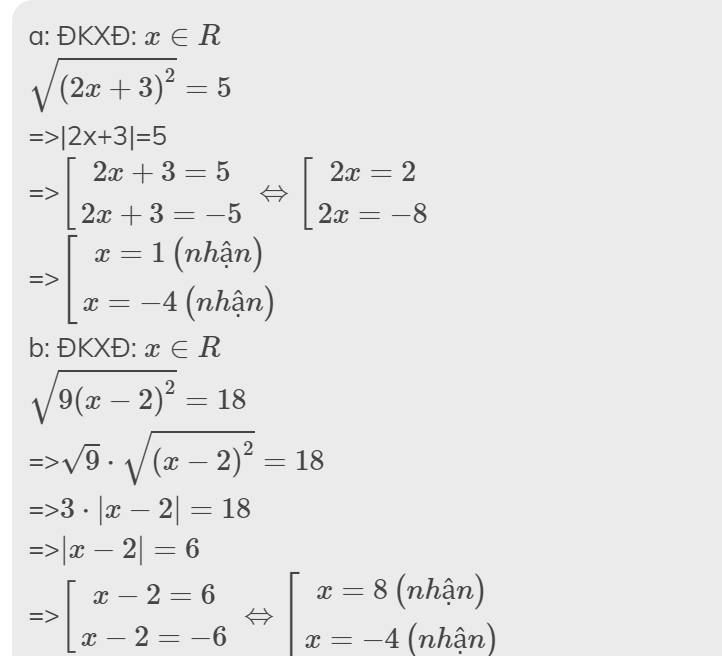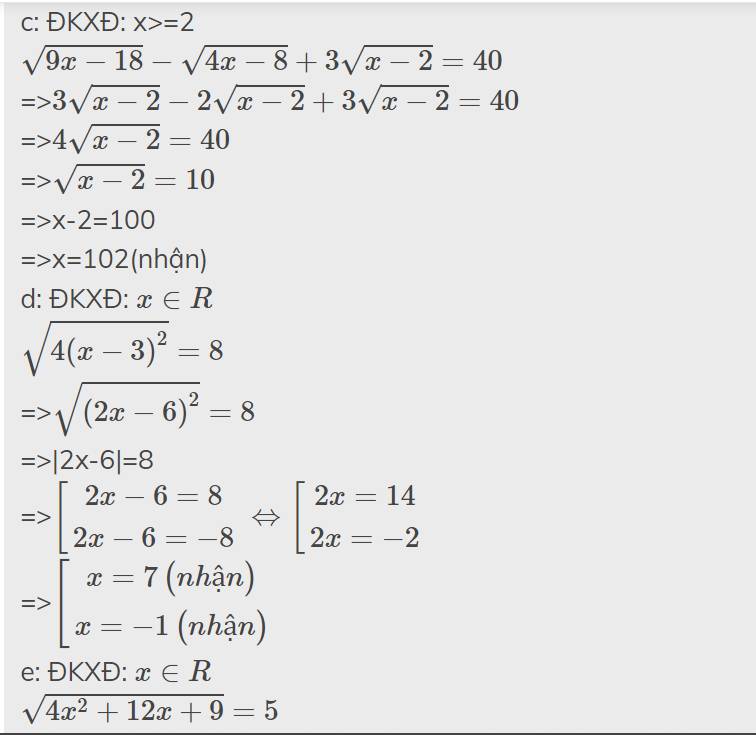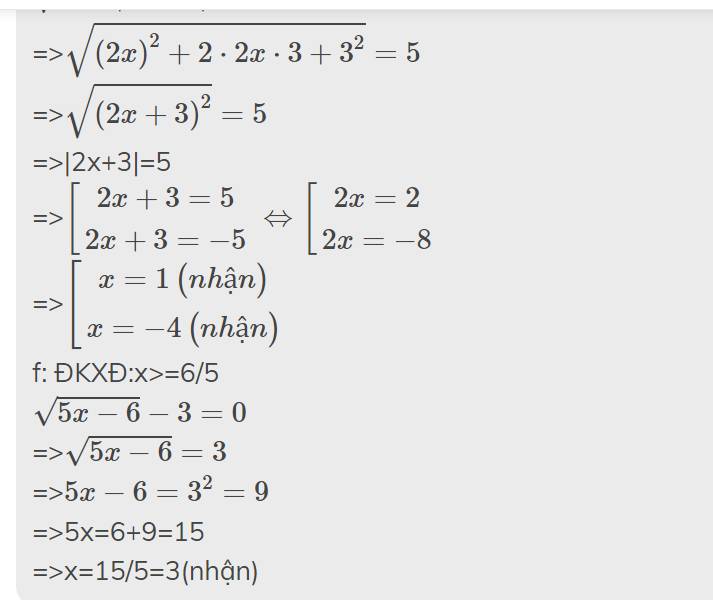\(\sqrt{9-2\sqrt{18}}+\sqrt{9+2\sqrt{18}}\)

Những câu hỏi liên quan
\(\sqrt{9-2\sqrt{18}}+\sqrt{9+2\sqrt{18}}\)
Bạn chú ý lần sau ghi đầy đủ đề bài! Những bài cộc lốc thế này lần sau mình sẽ xóa không thương tiếc nhé.
Coi đây là bài toán rút gọn.
Lời giải:
$\sqrt{9-2\sqrt{18}}+\sqrt{9+2\sqrt{18}}$
$=\sqrt{3+6-2\sqrt{3}.\sqrt{6}}+\sqrt{3+6+2\sqrt{3}.\sqrt{6}}$
$=\sqrt{(\sqrt{3}-\sqrt{6})^2}+\sqrt{(\sqrt{3}+\sqrt{6})^2}$
$=|\sqrt{3}-\sqrt{6}|+|\sqrt{3}+\sqrt{6}|$
$=\sqrt{6}-\sqrt{3}+\sqrt{3}+\sqrt{6}=2\sqrt{6}$
\(\sqrt{\left(2x+3\right)^2}=5\)
\(\sqrt{9.\left(x-2\right)^2}=18\)
\(\sqrt{9x-18}-\sqrt{4x-8}+3\sqrt{x-2}=40\)
\(\sqrt{4.\left(x-3\right)^2}=8\)
\(\sqrt{4x^2+12x+9}=5\)
\(\sqrt{5x-6}-3=0\)
a: ĐKXĐ: \(x\in R\)
\(\sqrt{\left(2x+3\right)^2}=5\)
=>|2x+3|=5
=>\(\left[{}\begin{matrix}2x+3=5\\2x+3=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=2\\2x=-8\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=1\left(nhận\right)\\x=-4\left(nhận\right)\end{matrix}\right.\)
b: ĐKXĐ: \(x\in R\)
\(\sqrt{9\left(x-2\right)^2}=18\)
=>\(\sqrt{9}\cdot\sqrt{\left(x-2\right)^2}=18\)
=>\(3\cdot\left|x-2\right|=18\)
=>\(\left|x-2\right|=6\)
=>\(\left[{}\begin{matrix}x-2=6\\x-2=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\left(nhận\right)\\x=-4\left(nhận\right)\end{matrix}\right.\)
c: ĐKXĐ: x>=2
\(\sqrt{9x-18}-\sqrt{4x-8}+3\sqrt{x-2}=40\)
=>\(3\sqrt{x-2}-2\sqrt{x-2}+3\sqrt{x-2}=40\)
=>\(4\sqrt{x-2}=40\)
=>\(\sqrt{x-2}=10\)
=>x-2=100
=>x=102(nhận)
d: ĐKXĐ: \(x\in R\)
\(\sqrt{4\left(x-3\right)^2}=8\)
=>\(\sqrt{\left(2x-6\right)^2}=8\)
=>|2x-6|=8
=>\(\left[{}\begin{matrix}2x-6=8\\2x-6=-8\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=14\\2x=-2\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=7\left(nhận\right)\\x=-1\left(nhận\right)\end{matrix}\right.\)
e: ĐKXĐ: \(x\in R\)
\(\sqrt{4x^2+12x+9}=5\)
=>\(\sqrt{\left(2x\right)^2+2\cdot2x\cdot3+3^2}=5\)
=>\(\sqrt{\left(2x+3\right)^2}=5\)
=>|2x+3|=5
=>\(\left[{}\begin{matrix}2x+3=5\\2x+3=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=2\\2x=-8\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=1\left(nhận\right)\\x=-4\left(nhận\right)\end{matrix}\right.\)
f: ĐKXĐ:x>=6/5
\(\sqrt{5x-6}-3=0\)
=>\(\sqrt{5x-6}=3\)
=>\(5x-6=3^2=9\)
=>5x=6+9=15
=>x=15/5=3(nhận)
Đúng 2
Bình luận (0)
a)\(\sqrt{5x-2}=3\)
b)\(\sqrt{x^2-4x+4}-5=0\)
c)\(3\sqrt{4x+8}-\sqrt{9x+18}+9.\sqrt{\dfrac{x+2}{9}}=\sqrt{72}\)
`a)sqrt{5x-2}=3(x>=2/5)`
`<=>5x-2=9`
`<=>5x=11`
`<=>x=11/5(tm)`
`b)sqrt{x^2-4x+4}-5=0`
`<=>\sqrt{(x-2)^2}=5`
`<=>|x-2|=5`
`<=>` \(\left[ \begin{array}{l}x-2=5\\x-2=-5\end{array} \right.\)
`<=>` \(\left[ \begin{array}{l}x=7\\x=-3\end{array} \right.\)
`c)3sqrt{4x+8}-sqrt{9x+18}+9sqrt{(x+2)/9}=sqrt{72}(x>=-2)`
`<=>6sqrt{x+2}-3sqrt{x+2}+3sqrt{x+2}=sqrt{72}`
`<=>6sqrt{x+2}=6sqrt2`
`<=>sqrt{x+2}=sqrt2`
`<=>x+2=2`
`<=>x=0(tm)`
Đúng 1
Bình luận (0)
\(a,ĐK:x\ge\dfrac{2}{5}\)
\(\Leftrightarrow5x-2=9\)
\(\Leftrightarrow5x=11\)
\(\Leftrightarrow x=\dfrac{11}{5}\)
\(b,\)
\(\Leftrightarrow x^2-5x+4=25\)
\(\Leftrightarrow x^2-5x-21=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5+\sqrt{109}}{2}\\x=\dfrac{5-\sqrt{109}}{2}\end{matrix}\right.\)
\(c,\)
\(\Leftrightarrow6\sqrt{x+2}-3\sqrt{x+2}+9\cdot\sqrt{\dfrac{x+2}{9}}=6\sqrt{2}\)
\(\Leftrightarrow2\sqrt{x+2}-\sqrt{x+2}+3\cdot\sqrt{\dfrac{x+2}{9}}=2\sqrt{2}\)
Đặt \(\sqrt{x+2}=a\) ta có (1)
\(2a-a+3\cdot\dfrac{a}{\sqrt{9}}=2\sqrt{2}\)
\(\Leftrightarrow a+3\cdot\dfrac{a}{3}=2\sqrt{2}\)
\(\Leftrightarrow2a=2\sqrt{2}\)
\(\Leftrightarrow a=\sqrt{2}\)
Thay \(a=\sqrt{2}\) vào (1) ta có
\(\sqrt{x+2}=\sqrt{2}\)
\(\Leftrightarrow x+2=2\)
\(\Leftrightarrow x=0\)
Đúng 0
Bình luận (0)
rút gọn biểu thức sau
D=\(\left(\sqrt{x-\sqrt{18}}-\sqrt{x+\sqrt{18}}\right)\sqrt{x+\sqrt{x^2-18}}\) với \(x\ge18\)
A=\(\sqrt{x+6\sqrt{x-9}}+\sqrt{x-6\sqrt{x-9}}\)
C=\(\dfrac{\sqrt{2-\sqrt{2-4-x^2}}\left[\sqrt{\left(2+x\right)^3}+\sqrt{\left(2-x\right)^3}\right]}{4-\sqrt{4-x^2}}\)
Giải Phương Trình
\(\sqrt{\left(2x+3\right)^2}=5\)
\(\sqrt{9\left(x-2\right)^2}=18\)
\(\sqrt{9x-18}-\sqrt{4x-8}+3\sqrt{x-2}=40\)
\(\sqrt{4.\left(x-3\right)^2}=8\)
\(\sqrt{5x-6}-3=0\)
tính
a, \(\sqrt{169}\) - \(\sqrt{225}\)
b \(\dfrac{\sqrt{144}}{9}\)
c \(\sqrt{18}\) \(\div\) \(\sqrt{2}\)
a: \(\sqrt{169}-\sqrt{225}\)
\(=\sqrt{13^2}-\sqrt{15^2}\)
=13-15
=-2
b: \(\dfrac{\sqrt{144}}{9}\)
\(=\dfrac{\sqrt{12^2}}{9}\)
\(=\dfrac{12}{9}=\dfrac{4}{3}\)
c: \(\sqrt{18}:\sqrt{2}=\sqrt{\dfrac{18}{2}}=\sqrt{9}=3\)
Đúng 1
Bình luận (0)
\(\sqrt{21-6\sqrt{6}}+\sqrt{9+2\sqrt{18}}-2\sqrt{6+3\sqrt{3}}\)
\(\sqrt{21-6\sqrt{6}}+\sqrt{9+2\sqrt{18}}-2\sqrt{6+3\sqrt{3}}\)
=\(\sqrt{21-2\sqrt{54}}+\sqrt{6+2\sqrt{18}+3}-\sqrt{4\cdot\left(6+3\sqrt{3}\right)}\)
=\(\sqrt{18-2\sqrt{54}+3}+\sqrt{6+2\sqrt{18}+3}-\sqrt{24+12\sqrt{3}}\)
=\(\sqrt{\left(\sqrt{18}-\sqrt{3}\right)^2}+\sqrt{\left(\sqrt{6}+\sqrt{3}\right)^2}-\sqrt{24+2\sqrt{108}}\)
=\(\left|\sqrt{18}-\sqrt{3}\right|+\left|\sqrt{6}+\sqrt{3}\right|-\sqrt{\sqrt{18}+2\sqrt{108}+\sqrt{6}}\)
=\(\left|\sqrt{18}-\sqrt{3}\right|+\left|\sqrt{6}+\sqrt{3}\right|-\sqrt{\left(\sqrt{18}+\sqrt{6}\right)^2}\)
=\(\left|\sqrt{18}-\sqrt{3}\right|+\left|\sqrt{6}+\sqrt{3}\right|-\left|\sqrt{18}-\sqrt{6}\right|\)
=\(\sqrt{18}-\sqrt{3}+\sqrt{6}+\sqrt{3}-\sqrt{18}-\sqrt{6}\)
= 0
Đúng 0
Bình luận (0)
Hic câu dưới bị giải nhầm nha bạn :<
\(\sqrt{21-6\sqrt{6}}+\sqrt{9+2\sqrt{18}}-2\sqrt{6+3\sqrt{3}}\)
=\(\sqrt{21-2\sqrt{54}}+\sqrt{6+2\sqrt{18}+3}-\sqrt{24+12\sqrt{3}}\)
=\(\sqrt{18-2\sqrt{54}+3}+\sqrt{6+2\sqrt{18}+3}-\sqrt{24+2\sqrt{108}}\)
=\(\sqrt{\left(\sqrt{18}-\sqrt{3}\right)^2}+\sqrt{\left(\sqrt{6}+\sqrt{3}\right)^2}-\sqrt{18+2\sqrt{108}+6}\)
=\(\sqrt{\left(\sqrt{18}-\sqrt{3}\right)^2}+\sqrt{\left(\sqrt{6}+\sqrt{3}\right)^2}-\sqrt{\left(\sqrt{18}+\sqrt{6}\right)^2}\)
=\(\left|\sqrt{18}-\sqrt{3}\right|+\left|\sqrt{6}+\sqrt{3}\right|-\left|\sqrt{18}+\sqrt{6}\right|\)
=\(\sqrt{18}-\sqrt{3}+\sqrt{6}+\sqrt{3}-\sqrt{18}-\sqrt{6}\)
=0
Đúng 0
Bình luận (0)
\(\sqrt{21-6\sqrt{6}}+\sqrt{9+2\sqrt{18}}-2\sqrt{6+3\sqrt{3}}\)
0 nhé bạn, thực ra thì tui bấm máy tính, chớ tui ms hc lớp 7 hà,
tích vs nhé
Đúng 0
Bình luận (0)
nếu bấm máy thì chắc chị giải đc rồi em :>
Đúng 0
Bình luận (0)
\(\sqrt{21-6\sqrt{6}}+\sqrt{9+2\sqrt{18}}-2\sqrt{6+3\sqrt{3}}\)
\(\sqrt{21-6\sqrt{6}}+\sqrt{9+2\sqrt{18}}-2\sqrt{6+3\sqrt{3}}\)
\(=3\sqrt{2}-\sqrt{3}+\sqrt{3}+\sqrt{6}-3\sqrt{2}-\sqrt{6}=0\)
Đúng 0
Bình luận (0)