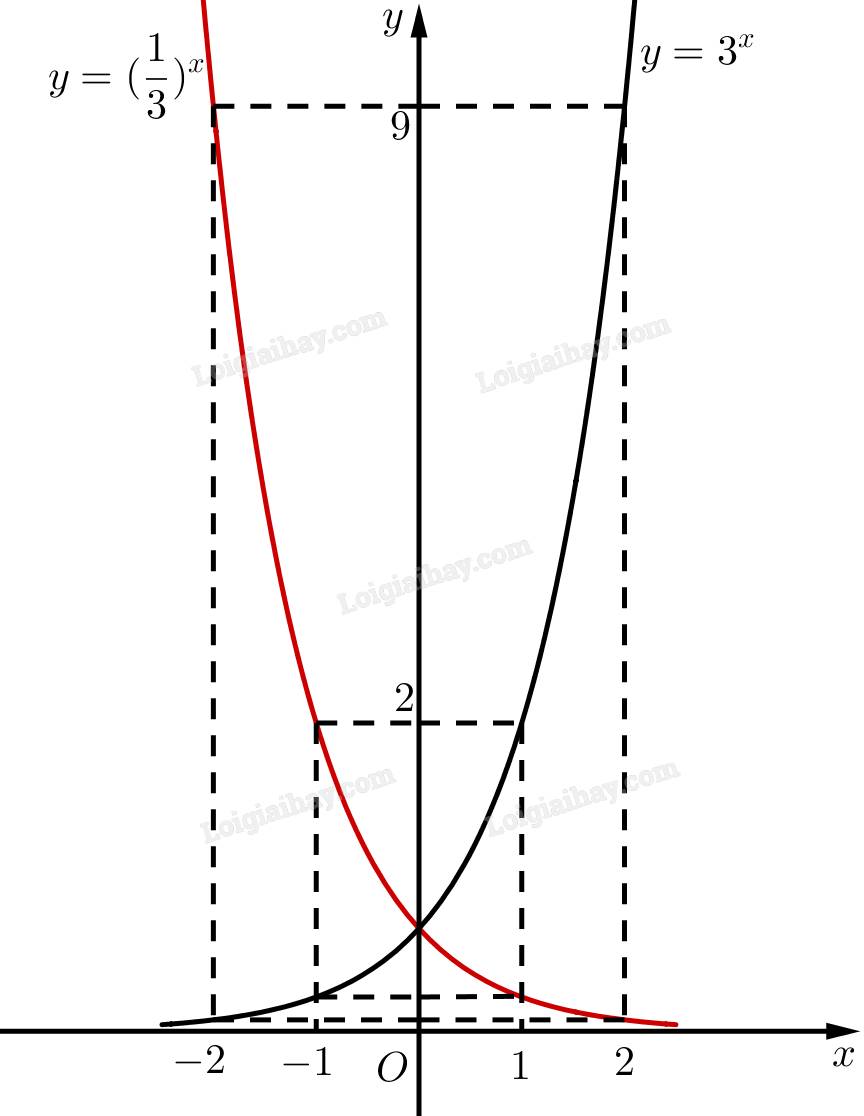
y =\(\frac{-1}{x+1}\) trên (-3;-2) và (2;3)
Xét tính đồng biến và nghịch biến của hàm số trên khoảng đã cho
\(\frac{x+1}{y^2+1}+\frac{y+1}{z^2+1}+\frac{z+1}{x^2+1}\)
Tìm giá trị lớn nhất của biểu thức trên, biết x+y+z=3
Cho hàm số \(y=\frac{1}{3}x^3-\frac{1}{2}\left(sina+cosa\right)x^2+\frac{3}{4}xsin2a\)Tìm a để y đồng biến trên R
lớp 8 chưa học lượng giác đâu bn
Mình quên mất. Đng học lp 8 nhưng học trc chương trình nên quên sửa lớp luôn
Ta có \(y'=x^2-\left(sina+cosa\right)x+\frac{3}{4}sin2a\)
Để y đồng biến trên R thì \(y'\ge0,\forall x\inℝ\)
\(\Leftrightarrow\Delta\le0\)
\(\Leftrightarrow\left(sina=cosa\right)^2-3sin2a\le0\)
\(\Leftrightarrow1-2sin2a\le0\)
\(\Leftrightarrow sin2a\ge\frac{1}{2}\Leftrightarrow\frac{\eta}{6}+k2\eta\le2a\le\frac{5\eta}{6}+k2\eta\)
\(\Leftrightarrow k\eta+\frac{\eta}{12}\le a\le\frac{5\eta}{12}+k\eta.\)
Tìm giá trị nhỏ nhất của biểu thức :
\(P=\frac{\sqrt{1+x^3+y^3}}{xy}+\frac{\sqrt{1+y^3+z^3}}{yz}+\frac{\sqrt{1+z^3+x^3}}{zx}\)
Trên miền \(D=\left\{\left(x;y;z\right):x>0;y>0;z>0;xyz=1\right\}\)
Áp dụng bất đẳng thức Cô - si, ta có :
\(P\ge\frac{\sqrt{3\sqrt[3]{x^3y^3}}}{xy}+\frac{\sqrt{3\sqrt[3]{y^3z^3}}}{yz}+\frac{\sqrt{3\sqrt[3]{z^3x^3}}}{zx}\)
\(\Rightarrow P\ge\sqrt{\frac{3}{xy}}+\sqrt{\frac{3}{yz}}+\sqrt{\frac{3}{zx}}\) (1)
Lại theo bất đẳng thức Cô si thì :
\(\sqrt{\frac{3}{xy}}+\sqrt{\frac{3}{yz}}+\sqrt{\frac{3}{zx}}\ge3\sqrt[3]{\sqrt{\frac{27}{\left(xyz\right)^2}}}\) (2)
Vì \(xyz=1\) nên ta có :
\(\sqrt{\frac{3}{xy}}+\sqrt{\frac{3}{yz}}+\sqrt{\frac{3}{zx}}\ge3\sqrt{3}\)
Khi \(x=y=z=1\Rightarrow P=3\sqrt{3}\)
Vậy giá trị nhỏ nhất của \(P=3\sqrt{3}\)
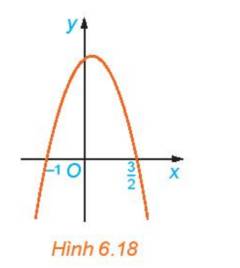
Cho đồ thị hàm số \(y = g(x) = - 2{x^3} + x + 3\) như Hình 6.18
a) Xét trên từng khoảng \(\left( { - \infty ; - 1} \right),\left( { - 1;\frac{3}{2}} \right),\left( {\frac{3}{2}; + \infty } \right)\), đồ thị nằm phía trên trục Ox hay nằm phía dưới trục Ox
b) Nhận xét về dấu của g(x) và dấu của hệ số a trên từng khoảng đó.
Ta có: hệ số a=-2<0
a) Nhìn vào đồ thị ta thấy
- Trên khoảng \(\left( { - \infty ; - 1} \right)\) đồ thị nằm phía dưới trục hoành
- Trên khoảng \(\left( { - 1;\frac{3}{2}} \right)\), đồ thị nằm phía trên trục hoành
- Trên khoảng \(\left( {\frac{3}{2}; + \infty } \right)\), đồ thị nằm phía dưới trục hoành
c) - Trên khoảng \(\left( { - \infty ; - 1} \right)\) đồ thị nằm phía dưới trục hoành => f(x)<0, cùng dầu với hệ số a
- Trên khoảng \(\left( { - 1;\frac{3}{2}} \right)\), đồ thị nằm phía trên trục hoành => f(x) >0, khác dấu với hệ số a
- Trên khoảng \(\left( {\frac{3}{2}; + \infty } \right)\), đồ thị nằm phía dưới trục hoành => f(x)<0, cùng dấu với hệ số a.
Có bao nhiêu số nguyên a thuộc [-2018,2018] để hàm số y=\(\frac{1}{3}x^3+\frac{1}{2}\left(sina-cosa\right)x^2-\frac{1}{2}\left(sin2a\right)x+1\) đồng biến trên R
CMR: \(\frac{1}{\left(x+y\right)^3}.\left(\frac{1}{x^3}+\frac{1}{y^3}\right)+\frac{3}{\left(x+y\right)^4}.\left(\frac{1}{x^2}+\frac{1}{y^2}\right)+\frac{6}{\left(x+y\right)^5}.\left(\frac{1}{x}+\frac{1}{y}\right)=\frac{1}{x^3y^3}\)
Rút gọn : \(\frac{1}{\left(x+y\right)^3}.\left(\frac{1}{x^3}+\frac{1}{y^3}\right)+\frac{3}{\left(x+y\right)^5}\left(\frac{1}{x^2}+\frac{1}{y^2}\right)+\frac{6}{\left(x+y\right)^5}\left(\frac{1}{x}+\frac{1}{y}\right)\)
Rút gọn \(\frac{1}{\left(x+y\right)^3}.\left(\frac{1}{x^3}+\frac{1}{y^3}\right)+\frac{3}{\left(x+y\right)^5}.\left(\frac{1}{x^2}+\frac{1}{y^2}\right)+\frac{6}{\left(x+y\right)^5}.\left(\frac{1}{x}+\frac{1}{y}\right)\)
\(\frac{^{x^2}+3xy+y^2}{x^3+2x^2y-xy^2-2y^3}=\frac{1}{x-y}\)
chứng minh đẳng thức trên :
Trên cùng một hệ trục toạ độ, vẽ đồ thị các hàm số \(y = {3^x}\) và \(y = {\left( {\frac{1}{3}} \right)^x}\).
tham khảo
Bảng giá trị:
-Hàm số \(y=3^x\)
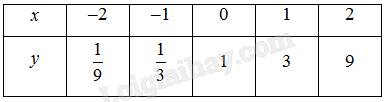
-Hàm số \(y=\left(\dfrac{1}{3}\right)^x\)
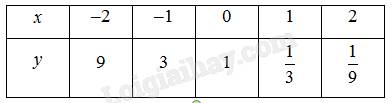
-Đồ thị