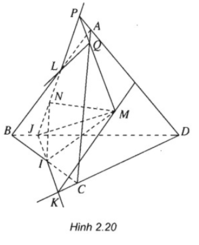
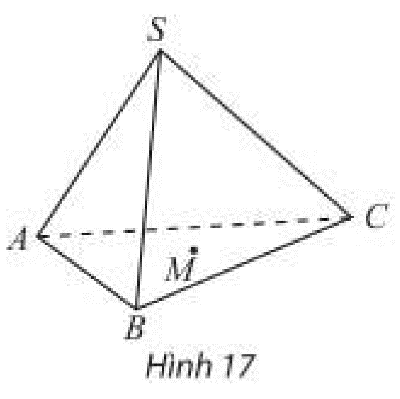
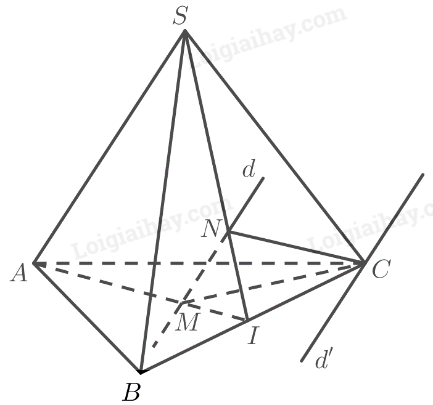
Cho hình chóp S.ABC và điểm M thuộc miên trong tam giác SBC. gọi E, F là 2 điểm thuộc AB và AC sao cho EF không song song BC
a) xác định giao tuyến của hai mặt phẳng (MEF) và (SBC)
b) Lấy N là điểm thuộc miền trong tam giác SAC sao cho NF cắt SA tại H. xác định giao tuyến của hai mặt phẳng (MNF) và (SAB)