cho tứ giavs ABCD GỌI E,F,I LẦN LƯỢT LÀ TRUNG ĐIỂM CỦA AD ,BC,AC
C/M EI//CD VÀ IF//AB
cho tứ giác ABCD gọi E, F,I lần lượt là trung điểm của AD ,BC,và AC
a) chứng minh EI//CD và IF//AB
cho tứ giác ABCD, gọi E,F,I lần lượt là trung điểm của AD,DC,AC
a, CM: EI//CD,IF//AD
b,CM: EF<(AB+CD)/2
Sửa đề: F là trung điểm của BC
a: Sửa đề: Cm IF//AB
Xét ΔACD có
E là trung điểm của AD
I là trung điểm của AC
Do đó: EI là đường trung bình
=>EI//CD và EI=CD/2
Xét ΔCAB có
I là trung điểm của AC
F là trung điểm của BC
Do đó: IF là đường trung bình
=>IF//AB và IF=AB/2
b: Xét ΔEIF có EF<IE+IF
nên \(FE< \dfrac{1}{2}\left(AB+CD\right)\)
Cho tứ giác ABCD , Gọi E,F,I theo thứ tự là trung điểm của AD,BC,AC . Chứng minh EI // CD, IF// AB
Ta có `E,F,I` là trung điểm của `AD,BC,AC`
`=> EI,IF` là đường trung bình của `\Delta ADC` và `\Delta ACB`
`=> EI////CD , EI = 1/2CD`
`=> IF////AB,IF=1/2AB`
Xét ΔADC có
E là trung điểm của AD(gt)
I là trung điểm của AC(gt)
Do đó: EI là đường trung bình của ΔADC(Định nghĩa đường trung bình của tam giác)
Suy ra: EI//DC
Xét ΔABC có
I là trung điểm của AC(gt)
F là trung điểm của BC(gt)
Do đó: IF là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra: IF//AB
cho tứ giác ABCD. Gọi E,F,I thheo thứ tự là trung điểm của AD, BC, AC. Chứng minh rằng
a) Ei//CD, IF//AB
a) Tam giác ACD có:
E là trung điểm của AD
I là trung điểm của AC
=> EI là ĐTB của tam giác ACD
=> EI // CD
Chứng minh tương tự IF là ĐTB của tam giác ABC
=> IF//AB
cho tứ giác ABCD ( AB//CD ) Gọi E,F,I lần lượt là trung điểm của AD,BC,AC .
A, cm : EI //CD ; IF // AB
b , cm EF < = (AB + CD) :2
C , tứ giác ABCD có thêm điều kiện GÌ thì EF = (AB+ CD ) :2
Cho tứ giác ABCD. Gọi E, F, I theo thứ tự là trung điểm của AD, BC, AC.
Chứng minh rằng:
a) EI//CD, IF//AB.
b)EF=<AB+CD/2
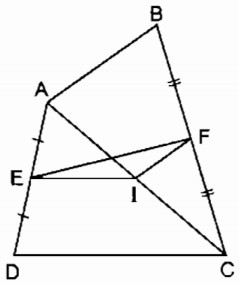
a) Trong tam giác ADC, ta có:
E là trung điểm của AD (gt)
I là trung điểm của AC (gt)
Nên EI là đường trung bình của ∆ ABC
⇒ EI // CD (tính chất đường trung bình của tam giác)
Và EI=CD/2
Trong tam giác ABC ta có:
I là trung điểm của AC
F là trung điểm của BC
Nên IF là đường trung bình của ∆ ABC
⇒ IF // AB (tính chất đường trung bình của tam giác)
Và IF=AB/2
b) Trong ∆ EIF ta có: EF ≤ EI + IF (dấu “=” xảy ra khi E, I, F thẳng hàng)
Mà EI=\(\dfrac{CD}{2}\); IF=\(\dfrac{AB}{2}\) (chứng minh trên) ⇒EF≤\(\dfrac{CD}{2}+\dfrac{AB}{2}\)
Vậy EF≤\(\dfrac{AB+CD}{2}\) (dấu bằng xảy ra khi AB // CD)
Tick nha 😘
a) Xét ΔACD có
I là trung điểm của AC
E là trung điểm của AD
Do đó: EI là đường trung bình của ΔACD
Suy ra: EI//CD
Xét ΔABC có
I là trung điểm của AC
F là trung điểm của BC
Do đó: IF là đường trung bình của ΔABC
Suy ra: IF//AB
Cho tứ giác ABCD. Gọi E, F, I là trung điểm của AD, BC, AC. Chứng minh rằng:
a) EI // CD; IF // AB.
b) EF ≤ (AB+CD)/2
3*đừng để ý
a: Xét ΔACD có
E là trung điểm của AD
I là trung điểm của AC
Do đó: EI là đường trung bình của ΔACD
Suy ra: EI//CD
Xét ΔACB có
F là trung điểm của BC
I là trung điểm của AC
Do đó: FI là đường trung bình của ΔACB
Suy ra: FI//AB
Cho tứ giác ABCD .Gọi E,F,I theo thứ tự là trung điểm của AD,BC,AC. Gọi M là trung điểm của ED.Từ M kẻ đường thẳng song song với EI,cắt AC tại N.
Chứng minhrằng:
a)EI//CD;IF//AB.
b)BiếtIN=3cm.TínhđộdàiđoạnthẳngIC.
\(a,\left\{{}\begin{matrix}AE=ED\\AI=IC\end{matrix}\right.\Rightarrow EI\) là đtb tam giác ADC \(\Rightarrow EI//CD\)
\(\left\{{}\begin{matrix}AI=IC\\BF=FC\end{matrix}\right.\Rightarrow IF\) là đtb tam giác ABC \(\Rightarrow IF//AB\)
\(b,\) Đề thiếu
Cho tứ giác ABCD .Gọi E,F,I theo thứ tự là trung điểm của AD,BC,AC. Gọi M là trung điểm của ED.Từ M kẻ đường thẳng song song với EI,cắt AC tại N.
Chứng minhrằng:
a)EI//CD;IF//AB.
b)BiếtIN=3cm.TínhđộdàiđoạnthẳngIC.