a.

\(P=cos120^0+cos120^0+cos120^0=-\dfrac{3}{2}\)

b.

\(A=\dfrac{\dfrac{sinx}{cosx}-\dfrac{cosx}{cosx}}{\dfrac{sinx}{cosx}+\dfrac{cosx}{cosx}}=\dfrac{tanx-1}{tanx+1}=\dfrac{2-1}{2+1}=\dfrac{1}{3}\)

c.

\(A=\dfrac{cos\left(720+30\right)+sin\left(360+60\right)}{sin\left(-360+30\right)-cos\left(-360-30\right)}=\dfrac{cos30+sin60}{sin30-cos30}=-3-\sqrt{3}\)

a: \(\overrightarrow{BA}-\overrightarrow{BC}=\overrightarrow{BA}+\overrightarrow{CB}=\overrightarrow{CA}\)

b: lấy điểm H sao cho \(\overrightarrow{AH}=\overrightarrow{GC}\)

\(\overrightarrow{AH}=\overrightarrow{GC}\)

=>AH//GC và AH=GC

Xét tứ giác AHCG có

AH//CG

AH=GC

Do đó: AHCG là hình bình hành

ΔABC đều có G là trọng tâm

nên \(AG=GB=GC=\dfrac{a\sqrt{3}}{3}\)

\(\left|\overrightarrow{AB}-\overrightarrow{GC}\right|=\left|\overrightarrow{AB}-\overrightarrow{AH}\right|\)

\(=\left|\overrightarrow{HA}+\overrightarrow{AB}\right|=\left|\overrightarrow{HB}\right|=HB\)

AHCG là hình bình hành

=>HC=AG và HC//AG

=>\(HC=\dfrac{a\sqrt{3}}{3}\)

ΔABC đều có G là trọng tâm

nên GB=GC=GA

GB=GC

AB=AC

Do đó: AG là đường trung trực của BC

=>AG\(\perp\)BC

mà CH//AG

nên CH\(\perp\)CB

=>ΔCHB vuông tại C

=>\(BH^2=HC^2+BC^2\)

=>\(BH^2=\left(\dfrac{a\sqrt{3}}{3}\right)^2+a^2=a^2+\dfrac{1}{3}a^2=\dfrac{4}{3}a^2\)

=>\(BH=a\cdot\dfrac{2\sqrt{3}}{3}\)

=>\(\left|\overrightarrow{AB}-\overrightarrow{GC}\right|=BH=\dfrac{2a\sqrt{3}}{3}\)

Gọi M là trung điểm của BC

Ta có: ΔABC đều

mà AM là đường trung tuyến

nên AM\(\perp\)BC tại M

Xét ΔAMB vuông tại M có \(sinB=\dfrac{AM}{AB}\)

=>\(\dfrac{AM}{1}=sin60=\dfrac{\sqrt{3}}{2}\)

=>\(AM=\dfrac{\sqrt{3}}{2}\)

Xét ΔABC có AM là đường trung tuyến

nên \(\overrightarrow{AB}+\overrightarrow{AC}=2\cdot\overrightarrow{AM}\)

=>\(\overrightarrow{AB}-\overrightarrow{CA}=2\cdot\overrightarrow{AM}\)

=>\(\left|\overrightarrow{AB}-\overrightarrow{CA}\right|=2\cdot AM=2\cdot\dfrac{\sqrt{3}}{2}=\sqrt{3}\)

=>A đúng, B và C đều sai

\(\left|\overrightarrow{AB}-\overrightarrow{AC}\right|\)

\(=\left|\overrightarrow{AB}+\overrightarrow{CA}\right|=\left|\overrightarrow{CB}\right|=CB=1\)

=>D sai

Do tam giác ABC vuông tại A và \(\widehat{B}=30^o\) \(\Rightarrow C=60^o\)

\(\Rightarrow\left(\overrightarrow{AB},\overrightarrow{BC}\right)=150^o;\)\(\left(\overrightarrow{BA},\overrightarrow{BC}\right)=30^o;\left(\overrightarrow{AC},\overrightarrow{CB}\right)=120^o\)

\(\left(\overrightarrow{AB},\overrightarrow{AC}\right)=90^o;\left(\overrightarrow{BC},\overrightarrow{BA}\right)=30^o\).Do vậy:

a) \(\cos\left(\overrightarrow{AB},\overrightarrow{BC}\right)+\sin\left(\overrightarrow{BA},\overrightarrow{BC}\right)+\tan\frac{\left(\overrightarrow{AC},\overrightarrow{CB}\right)}{2}\)

\(=\cos150^o+\sin30^o+\tan60^o\)

\(=-\frac{\sqrt{3}}{2}+\frac{1}{2}+\sqrt{3}\)

\(=\frac{\sqrt{3}+1}{2}\)

b) \(\sin\left(\overrightarrow{AB},\overrightarrow{AC}\right)+\cos\left(\overrightarrow{BC},\overrightarrow{AB}\right)+\cos\left(\overrightarrow{CA},\overrightarrow{BA}\right)\)

\(=\sin90^o+\cos30^o+\cos0^o\)

\(=1+\frac{\sqrt{3}}{2}\)

\(=\frac{2+\sqrt{3}}{2}\)

Dựng hình hình hành CADB.

Theo quy tắc hình bình hành: \(\overrightarrow{CA}+\overrightarrow{CB}=\overrightarrow{CD}\).
Vì vậy \(\left|\overrightarrow{CA}+\overrightarrow{CB}\right|=\left|\overrightarrow{CD}\right|=CD\);
Mặt khác \(\left|\overrightarrow{CA}-\overrightarrow{CB}\right|=\left|\overrightarrow{CA}+\overrightarrow{BC}\right|=\left|\overrightarrow{BA}\right|=BA\).
Suy ra: \(CD=AB\).
Hình bình hành CADB có hai đường chéo bằng nhau (\(CD=AB\) )nên hình bình hành CADB là hình chữ nhật.

Tham khảo:

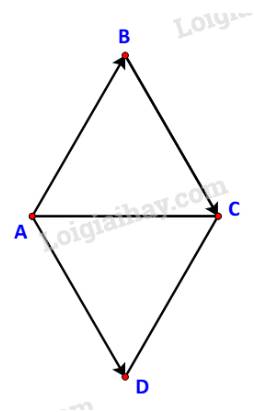
Lấy điểm D sao cho: \(\overrightarrow {AD}  = \overrightarrow {BC} \)

Khi đó ta có: \(\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right) = \widehat {BAD}\)

Dễ thấy ABCD là hình bình hành (hơn nữa còn là hình thoi) nên \(\widehat {BAD} = {180^o} - \widehat {ABC} = {120^o}\)

Vậy số đo góc \(\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right)\) là \({120^o}\).

Bài 3: 

Tham khảo:

1.

Đặt \(P=\left|\overrightarrow{AD}+3\overrightarrow{AB}\right|\Rightarrow P^2=AD^2+9AB^2+6\overrightarrow{AD}.\overrightarrow{AB}\)

\(=AD^2+9AB^2=10AB^2=10a^2\)

\(\Rightarrow P=a\sqrt{10}\)

2.

Tam giác ABC đều nên AM là trung tuyến đồng thời là đường cao \(\Rightarrow AM\perp BM\)

\(AM=\dfrac{a\sqrt{3}}{2}\) ; \(BM=\dfrac{a}{2}\)

\(T=\left|\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|\overrightarrow{MA}+2\overrightarrow{MB}\right|\)

\(\Rightarrow T^2=MA^2+4MB^2+4\overrightarrow{MA}.\overrightarrow{MB}=MA^2+4MB^2\)

\(=\left(\dfrac{a\sqrt{3}}{2}\right)^2+4\left(\dfrac{a}{2}\right)^2=\dfrac{7a^2}{4}\Rightarrow T=\dfrac{a\sqrt{7}}{2}\)

3.

\(T=\left|\overrightarrow{AB}+\overrightarrow{CG}\right|=\left|\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\right|=\left|\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{AB}\right|\)

\(=\left|\dfrac{4}{3}\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{AC}\right|\Rightarrow T^2=\dfrac{16}{9}AB^2+\dfrac{4}{9}AC^2-\dfrac{16}{9}\overrightarrow{AB}.\overrightarrow{AC}\)

\(=\dfrac{20}{9}AB^2-\dfrac{16}{9}AB^2.cos60^0=\dfrac{20}{9}a^2-\dfrac{16}{9}a^2.\dfrac{1}{2}=\dfrac{4}{3}a^2\)

\(\Rightarrow T=\dfrac{2a}{\sqrt{3}}\)