Điều kiện x ≠ 1 và x  ≠  - 1

Ta có:

Biểu thức dương khi x 2 + 2 x + 3 > 0

Ta có:  x 2 + 2 x + 3  =  x 2 + 2 x + 1 + 2  = x + 1 2 + 2 > 0 với mọi giá trị của x.

Vậy giá trị của biểu thức dương với mọi giá trị x  ≠  1 và x  ≠  - 1

\(a,P=5x\left(2-x\right)-\left(x+1\right)\left(x+9\right)\)

\(=10x-5x^2-\left(x^2+x+9x+9\right)\)

\(=10x-5x^2-x^2-x-9x-9\)

\(=\left(10x-x-9x\right)+\left(-5x^2-x^2\right)-9\)

\(=-6x^2-9\)

Ta thấy: \(x^2\ge0\forall x\)

\(\Rightarrow-6x^2\le0\forall x\)

\(\Rightarrow-6x^2-9\le-9< 0\forall x\)

hay \(P\) luôn nhận giá trị âm với mọi giá trị của biến \(x\).

\(b,Q=3x^2+x\left(x-4y\right)-2x\left(6-2y\right)+12x+1\)

\(=3x^2+x^2-4xy-12x+4xy+12x+1\)

\(=\left(3x^2+x^2\right)+\left(-4xy+4xy\right)+\left(-12x+12x\right)+1\)

\(=4x^2+1\)

Ta thấy: \(x^2\ge0\forall x\)

\(\Rightarrow4x^2\ge0\forall x\)

\(\Rightarrow4x^2+1\ge1>0\forall x\)

hay \(Q\) luôn nhận giá trị dương với mọi giá trị của biến \(x\) và \(y\).

#\(Toru\)

a)2x(2x+7)=4(2x+7)

    2x(2x+7)-4(2x+7)=0

    (2x+7)(2x-4)=0

\(\Rightarrow\orbr{\begin{cases}2x+7=0\\2x-4=0\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}x=-\frac{7}{2}\\x=2\end{cases}}\)

b)Ta có:x³-4x²+ax=x³-3x²-x²+ax

                           =x²(x-3)-x(x-a)

          Để x³-4x²+ax chia hết cho x-3 thì a=3

bạn làm luôn caai c đc không mkk sẽ tích cho bạn 

Điều kiện x  ≠  0 và x  ≠  -3

Ta có:

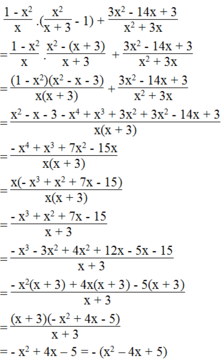
Vì x 2 - 4 x + 5 = x 2 - 4 x + 4 + 1 = x - 2 2 + 1 > 0 với mọi giá trị của x nên

- x 2 + 4 x - 5 = - x - 2 2 + 1 < 0 với mọi giá trị của x.

Vậy giá trị biểu thức luôn luôn âm với mọi giá trị x  ≠  0 và x ≠ -3

\(A=-x^2+3x-7\)

\(=-\left(x^2-3x+7\right)\)

\(=-\left(x^2-2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{19}{4}\right)\)

\(=-\left(x-\dfrac{3}{2}\right)^2-\dfrac{19}{4}< 0\forall x\)

\(3x-7-x^2=-\left(x^2-3x+\dfrac{9}{4}\right)-\dfrac{19}{4}=-\left(x-\dfrac{3}{2}\right)^2-\dfrac{19}{4}\le-\dfrac{19}{4}< 0\)

Ta có: \(x^2-3x+7=x^2-3x+\frac{9}{4}+\frac{19}{4}\)

\(=\left(x^2-3x+\frac{9}{4}\right)+\frac{19}{4}=\left(x-\frac{3}{2}\right)^2+\frac{19}{4}\)

Vì: \(\left(x-\frac{3}{2}\right)^2\ge0\forall x\)

\(\Rightarrow\left(x-\frac{3}{2}\right)^2+\frac{19}{4}\ge\frac{19}{4}>0\forall x\)

Hay : Biểu thức luôn dương với mọi giá trị của biến

=.= hok tốt!!

a: Sửa đề: 1/4x+x^2+2

x^2+1/4x+2

=x^2+2*x*1/8+1/64+127/64

=(x+1/8)^2+127/64>=127/64>0 với mọi x

=>ĐPCM

b: 2x^2+3x+1

=2(x^2+3/2x+1/2)

=2(x^2+2*x*3/4+9/16-1/16)

=2(x+3/4)^2-1/8 

Biểu thức này ko thể luôn dương nha bạn

c: 9x^2-12x+5

=9x^2-12x+4+1

=(3x-2)^2+1>=1>0 với mọi x

d: (x+2)^2+(x-2)^2

=x^2+4x+4+x^2-4x+4

=2x^2+8>=8>0 với mọi x

Bài 1) Chứng minh rằng các biểu thức sau luôn có giá trị âm với mọi giá trị của biến: 
a) 9x^2+12x-15 
=-(9x^2-12x+4+11) 
=-[(3x-2)^2+11] 
=-(3x-2)^2 - 11. 
Vì (3x-2)^2 không âm với mọi x suy ra -(3x-2)^2 nhỏ hơn hoặc bằng 0 vơi mọi x 
Do đó -[(3*x)-2]^2-11 < 0 với mọi giá trị của x. 
Hay -9*x^2 + 12*x -15 < 0 với mọi giá trị của x. 

b) -5 – (x-1)*(x+2) 
= -5-(x^2+x-2) 
=-5- (x^2+2x.1/2 +1/4 - 1/4-2) 
=-5-[(x-1/2)^2 -9/4] 
=-5-(x-1/2)^2 +9/4 
=-11/4 - (x-1/2)^2 
Vì (x-1/2)^2 không âm với mọi x suy ra -(x-1/2)^2 nhỏ hơn hoặc bằng 0 vơi mọi x 
Do đó -11/4 - (x-1/2)^2 < 0 với mọi giá trị của x. 
Hay -5 – (x-1)*(x+2) < 0 với mọi giá trị của x. 

Bài 2) 
a) x^4+x^2+2 
Vì x^4 +x^2 lớn hơn hoặc bằng 0 vơi mọi x 
suy ra x^4+x^2+2 >=2 
Hay x^4+x^2+2 luôn dương với mọi x. 

b) (x+3)*(x-11) + 2003 
= x^2-8x-33 +2003 
=x^2-8x+16b + 1954 
=(x-4)^2 + 1954 >=1954 
Vậy biểu thức luôn có giá trị dương với mọi giá trị của biến

bị ''rảnh'' ak ? 

tự hỏi r tự trả lời

1/ \(-9x^2+12x-15=\left(-9x^2+2.2.3x-4\right)-11\)

\(=-11-\left(3x-2\right)^2\le-11< 0\)

Câu b và câu 2 tương tự