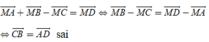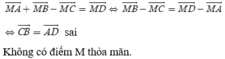cho hình vuông ABCD tìm tập hợp điểm M trong mặt phẳng sao cho MA+MB=MC+MD

Những câu hỏi liên quan
Cho hình vuông ABCD cạnh a, tâm O. Tìm tập hợp điểm M sao cho:
\(\overrightarrow{MA}.\overrightarrow{MB}+\overrightarrow{MC}.\overrightarrow{MD}=5a^2\)
Trong không gian Oxyz, cho bốn điểm A ( 2;0;0 ), B ( 0;4;0 ), C ( 0;0;6 ), D ( 2;4;6 ). Xét các mệnh đề sau:(I). Tập hợp các điểm M sao cho
M
A
→
+
M
B
→
M
C
→
+
M...
Đọc tiếp
Trong không gian Oxyz, cho bốn điểm A ( 2;0;0 ), B ( 0;4;0 ), C ( 0;0;6 ), D ( 2;4;6 ). Xét các mệnh đề sau:
(I). Tập hợp các điểm M sao cho M A → + M B → = M C → + M D → là một mặt phẳng
(II). Tập hợp các điểm M sao cho M A → + M B → + M C → + M D → = 4 là một mặt cầu tâm I(1;2;3) và bán kính R = 1
A. Chỉ (I)
B. Chỉ (II)
C. Không có
D. Cả (I) cả (II)
Xét mệnh đề (I):
Gọi I, J lần lượt là trung điểm AB, CD. Khi đó
M A → + M B → = M C → + M D → ⇔ 2 M I → = 2 M J → ⇔ M I = M J
Do đó tập hợp các điểm M là mặt phẳng trung trực của IJ
Vậy mệnh đề này đúng.
* Xét mệnh đề (II):
Gọi G là trọng tâm tứ diện ABCD
Khi đó M A → + M B → + M C → + M D → = 4 ⇔ 4 M G → = 4 ⇔ M G = 1
Do đó tập hợp các điểm M là mặt cầu tâm G ( 1;2;3 ) và bán kính R = 1
Vậy mệnh đề này đúng
Đáp án D
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có cạnh bằng 6 cm ( với mọi điểm M trong mặt phẳng )
a, cm : \(\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}\)
\(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{BM}+\overrightarrow{MA}=\overrightarrow{BA}\)(2)
\(\overrightarrow{MD}-\overrightarrow{MC}=\overrightarrow{CM}+\overrightarrow{MD}=\overrightarrow{CD}\)(1)
Vì ABCD là hình vuông nên \(\overrightarrow{BA}=\overrightarrow{CD}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{MD}-\overrightarrow{MC}\)
=>\(\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}\)
Đúng 0
Bình luận (0)
Câu 38. Cho tam giác ABC. Tìm tập hợp điểm M thỏa mãn 3|MA+MB| 2 |MA+ MB + MC| Câu 37. Trong mặt phẳng Oxy, cho tam giác ABC, có A(1;5), B(-2;2), C(3; - 1) . a. Tìm tọa độ điểm D sao cho ABCD là hình bình hành. b. Tìm tọa độ điểm E sao cho A là trung điểm đoạn BE. c. Tìm tọa độ điểm F sao cho B là trọng tâm tam giác ACF.
Đọc tiếp
Câu 38. Cho tam giác ABC. Tìm tập hợp điểm M thỏa mãn 3|MA+MB| =2 |MA+ MB + MC| Câu 37. Trong mặt phẳng Oxy, cho tam giác ABC, có A(1;5), B(-2;2), C(3; - 1) . a. Tìm tọa độ điểm D sao cho ABCD là hình bình hành. b. Tìm tọa độ điểm E sao cho A là trung điểm đoạn BE. c. Tìm tọa độ điểm F sao cho B là trọng tâm tam giác ACF.
38.
Gọi I là trung điểm AB và G là trọng tâm tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}\\\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\end{matrix}\right.\)
\(3\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=2\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|\)
\(\Leftrightarrow3.\left|2\overrightarrow{MI}\right|=3\left|\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right|\)
\(\Leftrightarrow6\left|\overrightarrow{MI}\right|=2.\left|3\overrightarrow{MG}\right|\)
\(\Leftrightarrow6\left|\overrightarrow{MI}\right|=6\left|\overrightarrow{MG}\right|\)
\(\Leftrightarrow\left|\overrightarrow{MI}\right|=\left|\overrightarrow{MG}\right|\)
\(\Leftrightarrow MI=MG\)
\(\Rightarrow\) Tập hợp M là đường trung trực của đoạn thẳng IG
Đúng 1
Bình luận (0)
Cho ABCD là hình bình hành. Chứng minh \(\overrightarrow {MB} - \overrightarrow {MA} = \overrightarrow {MC} - \overrightarrow {MD} \) với mỗi điểm M trong mặt phẳng.
Ta có: \(\overrightarrow {AM} = - \overrightarrow {MA} ,\;\overrightarrow {DM} = - \overrightarrow {MD} \)
\( \Rightarrow \overrightarrow {MB} - \overrightarrow {MA} = \overrightarrow {MB} + \overrightarrow {AM} = \overrightarrow {AM} + \overrightarrow {MB} = \overrightarrow {AB} \)
Tương tự ta có: \(\overrightarrow {MC} - \overrightarrow {MD} = \overrightarrow {MC} + \overrightarrow {DM} = \overrightarrow {DM} + \overrightarrow {MC} = \overrightarrow {DC} \)
Mà \(\overrightarrow {AB} = \overrightarrow {DC} \)(do ABCD là hình bình hành)
\( \Rightarrow \overrightarrow {MB} - \overrightarrow {MA} = \overrightarrow {MC} - \overrightarrow {MD} \) (đpcm)
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD cố định. Tìm tập hợp điểm M sao cho:
a) MA\(^2\)+ MC\(^2\)= MB\(^2\)+ MD\(^2\)
b) MA + MC = MB + MD.
Cho tứ giác ABCD, tìm tập hợp điểm M sao cho: \(2\overrightarrow{MA}+3\overrightarrow{MB}-\overrightarrow{MC}+4\overrightarrow{MD}=\overrightarrow{0}\)
Cho hình bình hành ABCD. Tập hợp các điểm M thỏa mãn
M
A
→
+
M
B
→
-
M
C
→
M
D
→
A. một đường tròn. B. một đường thẳng. C. tập rỗng. D. một đoạn thẳng...
Đọc tiếp
Cho hình bình hành ABCD. Tập hợp các điểm M thỏa mãn M A → + M B → - M C → = M D →
A. một đường tròn.
B. một đường thẳng.
C. tập rỗng.
D. một đoạn thẳng.
Cho hình bình hành ABCD. Tập hợp các điểm M thỏa mãn
M
A
→
+
M
B
→
-
M
C
→
M
D
→
là? A. một đường tròn. B. một đường thẳng. C. tập rỗng. D. một...
Đọc tiếp
Cho hình bình hành ABCD. Tập hợp các điểm M thỏa mãn M A → + M B → - M C → = M D → là?
A. một đường tròn.
B. một đường thẳng.
C. tập rỗng.
D. một đoạn thẳng.