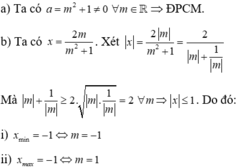a: Khi m=-1 thì hệ phương trình sẽ trở thành:

\(\left\{{}\begin{matrix}-x+y-3=3\\x-y-2\cdot\left(-1\right)+1=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}-x+y=6\\x-y=-3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}0x=3\left(vôlý\right)\\x-y=-3\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\varnothing\)

b: \(\left\{{}\begin{matrix}mx+y-3=3\\x+my-2m+1=0\end{matrix}\right.\)(1)

=>\(\left\{{}\begin{matrix}mx+y=6\\x+my=2m-1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=6-mx\\x+m\left(6-mx\right)=2m-1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x+6m-m^2x=2m-1\\y=6-mx\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x\left(1-m^2\right)=-4m-1\\y=6-mx\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x\left(m^2-1\right)=4m+1\\y=6-mx\end{matrix}\right.\)

TH1: m=1

Hệ phương trình (1) sẽ trở thành: 

\(\left\{{}\begin{matrix}x\cdot0=4\cdot1+1=5\\y=6-mx\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\varnothing\)

=>Loại

TH2: m=-1

Hệ phương trình (1) sẽ trở thành:

\(\left\{{}\begin{matrix}x\cdot0=-4+1=-3\\y=6-mx\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\varnothing\)

=>Loại

Th3: \(m\notin\left\{1;-1\right\}\)

Hệ phương trình (1) sẽ tương đương với \(\left\{{}\begin{matrix}x=\dfrac{4m+1}{m^2-1}\\y=6-mx=\dfrac{6\left(m^2-1\right)-m\left(4m+1\right)}{m^2-1}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=\dfrac{4m+1}{m^2-1}\\y=\dfrac{6m^2-6-4m^2-m}{m^2-1}=\dfrac{2m^2-m-6}{m^2-1}\end{matrix}\right.\)

Để hệ có nghiệm duy nhất thì m/1<>1/m

=>\(m^2\ne1\)

=>\(m\notin\left\{1;-1\right\}\)

Để x nguyên thì \(4m+1⋮m^2-1\)

=>\(\left(4m+1\right)\left(4m-1\right)⋮m^2-1\)

=>\(16m^2-1⋮m^2-1\)

=>\(16m^2-16+15⋮m^2-1\)

=>\(m^2-1\inƯ\left(15\right)\)

=>\(m^2-1\in\left\{1;-1;3;-3;5;-5;15;-15\right\}\)

=>\(m^2\in\left\{2;0;4;6;16\right\}\)

=>\(m\in\left\{\sqrt{2};-\sqrt{2};0;2;-2;\sqrt{6};-\sqrt{6};4;-4\right\}\)

mà m nguyên

nên \(m\in\left\{0;2;4;-2;-4\right\}\left(2\right)\)

Để y nguyên thì \(2m^2-m-6⋮m^2-1\)

=>\(2m^2-2-m-4⋮m^2-1\)

=>\(m+4⋮m^2-1\)

=>\(\left(m+4\right)\left(m-4\right)⋮m^2-1\)

=>\(m^2-16⋮m^2-1\)

=>\(m^2-1-15⋮m^2-1\)

=>\(m^2-1\inƯ\left(-15\right)\)

=>\(m^2-1\in\left\{1;-1;3;-3;5;-5;15;-15\right\}\)

=>\(m^2\in\left\{2;0;4;6;16\right\}\)

=>\(m\in\left\{\sqrt{2};-\sqrt{2};0;2;-2;\sqrt{6};-\sqrt{6};4;-4\right\}\)

mà m nguyên

nên \(m\in\left\{0;2;4;-2;-4\right\}\left(3\right)\)

Từ (2),(3) suy ra \(m\in\left\{0;2;4;-2;-4\right\}\)

Thử lại, ta sẽ thấy m=4;m=-2 không thỏa mãn x nguyên; m=4;m=-2 không thỏa mãn y nguyên

=>\(m\in\left\{0;2;-4\right\}\)

1) điều kiện của m: m khác 5/2

thế x=2 vào pt1 ta đc:

(2m-5)*4 - 4(m-1)+3=0 <=> 8m-20-4m+4+3=0<=> 4m = 13 <=> m=13/4 (nhận)

lập △'=[-(m-1)]²-*(2m-5)*3 = (m-4)²

vì (m-4)² ≥ 0 nên phương trình có nghiệm kép => x1= x2 =2

3) vì △'≥0 với mọi m nên phương trình đã cho có nghiệm với mọi m

ĐK: \(-2\le x\le2\)

Đặt \(\sqrt{x+2}+\sqrt{2-x}=t\left(2\le t\le2\sqrt{2}\right)\)

Phương trình đã cho trở thành:

\(t+t^2-4+2m+3=0\)

\(\Leftrightarrow2m=f\left(t\right)=-t^2-t+1\)

Phương trình đã cho có nghiệm khi \(minf\left(t\right)\le2m\le maxf\left(t\right)\)

\(\Leftrightarrow-7-2\sqrt{2}\le2m\le-5\)

\(\Leftrightarrow\dfrac{-7-2\sqrt{2}}{2}\le m\le-\dfrac{5}{2}\)

a: Khi m=4 thì (1) sẽ là:

x^2-6x-7=0

=>x=7 hoặc x=-1

b: Sửa đề: 2x1+3x2=-11

x1+x2=2m-2

=>2x1+3x2=-11 và 2x1+2x2=4m-4

=>x2=-11-4m+4=-4m-7 và x1=2m-2+4m+7=6m+5

x1*x2=-2m+1

=>-24m^2-20m-42m-35+2m-1=0

=>-24m^2-60m-34=0

=>\(m=\dfrac{-15\pm\sqrt{21}}{12}\)

Chọn D.

Đặt t = 3^x > 0, phương trình trở thành t² - (m - 1) t + 2m = 0 (*)

Yêu cầu bài toán thành phương trình (*)  có đúng một nghiệm dương.

+ (*)  có nghiệm kép dương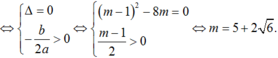 

+ (*)  có hai nghiệm trái dấu khi đó; 2m < 0 hay m < 0.

Vậy m < 0 hoặc  thỏa yêu cầu bài toán.

a) m²+1\(\ge\)1 \(\forall\)m, suy ra phương trình đã cho là phương trình bậc nhất một ẩn với mọi m.

b) Nghiệm của phương trình đã cho là x=\(\dfrac{2m}{m^2+1}\) (*).

Áp dụng BĐT Co-si cho hai số dương m² và 1, ta có:

m²+1\(\ge\)2\(\sqrt{m^2.1}\)=2|m|.

Dấu "=" xảy ra khi và chỉ khi m²=1 \(\Rightarrow\) m=\(\pm\)1.

Với m=1, x=1.

Với m=-1, x=-1.

So sánh hai giá trị của x, ta kết luận: giá trị m cần tìm là m=1.