\(\Leftrightarrow y'=0\) 

có 2 nghiệm phân biệt \(x_1,x_2\) thỏa mãn \(x_1\)<\(x_2\)<1

\(\Leftrightarrow\)\(\begin{cases}\Delta'=4m^2-m-5>0\\f\left(1\right)=-5m+7>0\\\frac{S}{2}=\frac{2m-1}{3}<1\end{cases}\)\(\Leftrightarrow\)\(\frac{5}{4}\)<m<\(\frac{7}{5}\)

Đặt (d): y=(m-2)x+m+1

Để (d): y=(m-2)x+m+1 là hàm số bậc nhất thì m-2<>0

=>m<>2

Tọa độ giao điểm của (d) với trục hoành là:

\(\left\{{}\begin{matrix}y=0\\\left(m-2\right)x+m+1=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=0\\x\left(m-2\right)=-m-1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=0\\x=\dfrac{-m-1}{m-2}\end{matrix}\right.\)

Để hoành độ nhỏ hơn -1 thì \(\dfrac{-m-1}{m-2}< -1\)

=>\(\dfrac{m+1}{m-2}>1\)

=>\(\dfrac{m+1-m+2}{m-2}>0\)

=>\(\dfrac{3}{m-2}>0\)

=>m-2>0

=>m>2

=>\(\left\{{}\begin{matrix}y=0\\x=\dfrac{-m-1}{m-2}\end{matrix}\right.\)

phương trình hoành độ giao điểm của f(x) với y = -1 là

x⁴ - (3m + 2)x² + 3m = -1

⇔ x⁴ - (3m + 2)x² + 3m + 1 = 0 (1)

Đặt x² = t (ĐK : t ≥ 0)

Phương trình trở thành 

t² - (3m + 2)t + 3m + 1 = 0 (2)

Để (1) có 4 nghiệm phân biệt nhỏ hơn 2 thì (2) có 2 nghiệm phân biệt thỏa mãn 0 < t < 4

⇒ \(\left\{{}\begin{matrix}9-9m< 0\\3m+1>0\end{matrix}\right.\) (cái này bạn vẽ bảng biến thiên ra là xong)

⇒ \(\dfrac{-1}{3}< m< 1\) 

Vậy tập hợp giá trị m cần tìm là \(\left(\dfrac{-1}{3};1\right)\)

Câu 2: 

Thay x=0 và y=-3 vào (d), ta được:

m+2=-3

hay m=-5

Đáp án là A.

          • y ' = 3 x 2 − 6 m + 1 x + 3 m − 1 2 ;    y ' ' = 6 x − 6 m + 1  

          • Hàm số đạt cực trị tại điểm x=1 thì  

y ' 1 = 0 y ' ' 1 ≠ 0 ⇔ m 2 − 4 m = 0 m ≠ 0 ⇔ m = 0 m = 4 m ≠ 0 ⇒ m = 4.

          * Ghi chú: Không có đáp án, sửa lại đáp A thành  

(d) cắt trục hoành độ là 1: 

⇒ \(x=1\) 

Và hàm số: \(y=0\)

Thay \(x=1\) tại giá trị hàm số \(y=0\)

Ta có: 

\(y=\left(m-3\right)\cdot1+3m-1=0\)

\(\Leftrightarrow\left(m-3\right)+3m-1=0\)

\(\Leftrightarrow m-3+3m-1=0\)

\(\Leftrightarrow4m-4=0\)

\(\Leftrightarrow4m=4\)

\(\Leftrightarrow m=1\)

Vậy: ...

3: Thay x=1 và y=0 vào (d), ta được:

m-3+3m-1=0

=>4m-4=0

=>m=1

Vì đồ thị hàm số đi qua điểm (5;-3) nên x=5, y=-3

Thay x=5, y=-3 vào CTHS y=(3m-1)x+4n-2 ta có

      \(\Rightarrow\)   -3=(3m-1)5 +4n -2

        \(\Rightarrow\) -3=15m-5+4n-2

     \(\Rightarrow\)    15m+3n=-4

   \(\Rightarrow\)       m=\(\frac{-4-3n}{15}\)(1)

 Vì đồ thị hàm số cắt trục hoành tại điểm có tung độ là -2 nên x=-2 , y=0

Thay x=-2, y=0 vào CTHS y=(3m-1)x+4n-2 ta có

         0=(3m-1)-2+4n-2

   \(\Rightarrow\)0=-6m+2+4n-2

  \(\Rightarrow\)-6m+4n=0

 \(\Rightarrow\)m=\(\frac{4n}{-6}\)(2)

Từ 1 và 2 ta có

      \(\frac{-4-3n}{15}\)=\(\frac{4n}{-6}\)

\(\Leftrightarrow\)24+18n=60n

\(\Leftrightarrow\)24=42n

\(\Leftrightarrow\)n=1,75

 Thay n=1,75 vào (1) ta có

       m=\(\frac{-4-3\cdot1,75}{15}\)

\(\Leftrightarrow\)m=\(\frac{-37}{60}\)

 Vậy n=1,75 ;m=\(\frac{-37}{60}\)thì thoả mãn yêu cầu của đề bài

CHÚC BẠN HỌC TỐT

- Hàm số đã cho xác định với ∀x ∈ R.

- ta có:

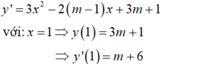
- Phương trình tiếp tuyến tại điểm có hoành độ x = 1 là:

   y = (m+ 6)(x – 1) + 3m + 1

- Tiếp tuyến này đi qua A(2; - 1) nên có:

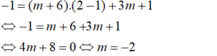
- Vậy m = -2 là giá trị cần tìm.