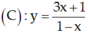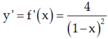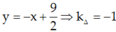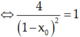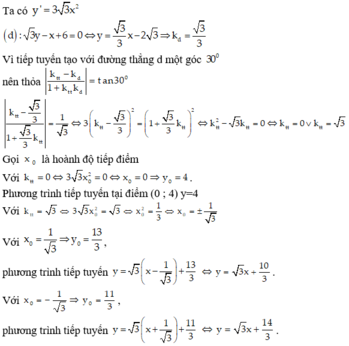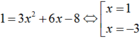Bài 1. Cho đường cong (C) : y = \(\frac{3x+1}{1-x}\) .Viết phương trình tiếp tuyến của (C) biết tiếp tuyến tạo với đường thẳng (Δ) : x\(-\)2y+5 = 0 một góc 30\(^{\theta}\)
Bài 2. Cho hàm số y = \(\sin x+2\cos x+\left(2m-5\right)x-1\) (với m là tham số). Tìm tất cả các giá trị của tham số m để hàm số đã cho đồng biến trên tập xác định của nó.
Bài 3. Cho hàm số y = \(x^4+mx^2-3\) (với m là tham số). Tìm tất cả các giá trị của tham số m để hàm số đã cho đồng biến trên khoảng (0;+\(\infty\))
Mình rất cần sự giúp đỡ của mọi người, mình cảm ơn trước ạ :'((((