a: Xét (O) có

CA,CM là tiếp tuyến

nênCA=CM và OC là phân giác của góc AOM(1)

mà OA=OM

nên OC là trung trực của AM

=>OC vuông góc với AM

Xét (O) có

DM,DB là tiếp tuyến

nên DM=DB và OD là phân giác của góc MOB(2)

Xét (O)có

ΔAMB nội tiếp

AB là đường kính

Do đó: ΔAMB vuông tại M

=>MB vuông góc MA

=>MB//OC

b: Từ (1), (2) suy ra góc COD=1/2*180=90 độ

=>OC vuông góc với OD

mà OM vuông góc DC

nên MC*MD=OM^2

=>AC*BD=R^2

c: Gọi H là trung điểm của CD

Xét hình thang ABDC có

H,O lần lượtlà trung điểm của CD,AB

nên HO là đường trung bình

=>HO//AC//BD

=>HO vuông góc với AB

=>AB là tiếp tuyến của (H)

a: Xét (O) có

CM,CA là tiếp tuyến

Do đó: CM=CA và OC là phân giác của \(\widehat{AOM}\)

=>\(\widehat{COM}=\dfrac{1}{2}\cdot\widehat{MOA}\)

Xét (O) có

DM,DB là tiếp tuyến

Do đó: DM=DB và OD là phân giác của \(\widehat{MOB}\)

=>\(\widehat{MOD}=\dfrac{1}{2}\cdot\widehat{MOB}\)

\(\widehat{COD}=\widehat{COM}+\widehat{DOM}\)

\(=\dfrac{1}{2}\cdot\widehat{MOA}+\dfrac{1}{2}\cdot\widehat{MOB}\)

\(=\dfrac{1}{2}\left(\widehat{MOA}+\widehat{MOB}\right)=\dfrac{1}{2}\cdot180^0=90^0\)

CD=CM+MD

mà CM=CA và DM=DB

nên CD=CA+DB

b: Xét ΔOCD vuông tại O có OM là đường cao

nên \(OM^2=CM\cdot MD\)

=>\(AC\cdot BD=R^2\) 

c: CM=CA

OM=OA

Do đó: CO là đường trung trực của AM

=>CO\(\perp\)AM tại E

DM=DB

OM=OB

Do đó: OD là đường trung trực của MB

=>OD\(\perp\)MB tại F

Xét tứ giác MEOF có

\(\widehat{MEO}=\widehat{MFO}=\widehat{FOE}=90^0\)

=>MEOF là hình chữ nhật

=>EF=OM=R

a: Xét tứ giác OBME có 

\(\widehat{OBM}+\widehat{OEM}=180^0\)

Do đó: OBME là tứ giác nội tiếp

a: Xét (O) có

MC,MB là các tiếp tuyến

Do đó: MC=MB

=>M nằm trên đường trung trực của BC(1)

Ta có: OB=OC

=>O nằm trên đường trung trực của BC(2)

Từ (1) và (2) suy ra MO là đường trung trực của BC

=>MO\(\perp\)BC

b: Xét (O) có

ΔACB nội tiếp

AB là đường kính

Do đó: ΔACB vuông tại C

=>BC\(\perp\)AC tại C

=>BC\(\perp\)AN tại C

=>ΔBNC vuông tại C

Ta có: \(\widehat{NCM}+\widehat{MCB}=\widehat{NCB}=90^0\)

\(\widehat{CNM}+\widehat{CBM}=90^0\)(ΔNCB vuông tại C)

mà \(\widehat{MCB}=\widehat{MBC}\)

nên \(\widehat{NCM}=\widehat{CNM}\)

=>ΔMNC cân tại M

=>MN=MC

mà MC=MB

nên MN=MB

=>M là trung điểm của BN

c: ta có: CH\(\perp\)AB

NB\(\perp\)BA

Do đó: CH//NB

Xét ΔANM có CI//NM

nên \(\dfrac{CI}{NM}=\dfrac{AI}{AM}\left(3\right)\)

Xét ΔAMB có IH//MB

nên \(\dfrac{IH}{MB}=\dfrac{AI}{AM}\left(4\right)\)

Từ (3) và (4) suy ra \(\dfrac{CI}{NM}=\dfrac{IH}{MB}\)

mà NM=MB

nên CI=IH

=>I là trung điểm của CH

a: Xét (O) có

MA,MH là tiếp tuyến

nên MA=MH

mà OA=OH

nên OM là phân giác của góc AOH(1) và HM=MA

Xét (O) có

NH,NB là tiếp tuyến

nên NH=NB và ON là phân giác của góc HOB(2)

Từ (1), (2) suy ra góc MON=1/2*180=90 độ

AM*BN=HM*HN=OH^2=R^2

b: AM+BN=HN+HM>=2*OH=AB

Dấu = xảy ra khi MN=AB

=>H trùng với O

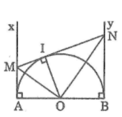
Tam giác OMN vuông tại O có OI ⊥ MN (tính chất tiếp tuyến)

Theo hệ thức lượng trong tam giác vuông, ta có:

O I 2 = MI.NI

Mà: MI = MA, NI = NB (chứng minh trên)

Suy ra : AM.BN =  O I 2  =  R 2

a: Xét (O) có

CE là tiếp tuyến

CA là tiếp tuyến

Do đó: CE=CA

Xét (O) có

DE là tiếp tuyến

DB là tiếp tuyến

Do đó: DE=DB

Ta có: DE+CE=DC

nên CD=AC+BD