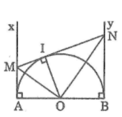
Tam giác OMN vuông tại O có OI ⊥ MN (tính chất tiếp tuyến)
Theo hệ thức lượng trong tam giác vuông, ta có:
O I 2 = MI.NI
Mà: MI = MA, NI = NB (chứng minh trên)
Suy ra : AM.BN = O I 2 = R 2

Tam giác OMN vuông tại O có OI ⊥ MN (tính chất tiếp tuyến)
Theo hệ thức lượng trong tam giác vuông, ta có:
O I 2 = MI.NI
Mà: MI = MA, NI = NB (chứng minh trên)
Suy ra : AM.BN = O I 2 = R 2
Cho nửa đường tròn tâm O đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi M là điểm bất kì thuộc tia Ax. Qua M kẻ tiếp tuyến với nửa đường tròn, cắt By ở N. Chứng minh rằng MN = AM + BN
Cho nửa đường tròn tâm O, đường kính AB. gọi Ax, By vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng 1 nửa mặt phẳng bờ AB). M là điểm bất kì thuộc Ax. Từ M kẻ tiếp tuyến với nửa đường tròn cắt By ở N.
a) Tính góc MON
b) Chứng minh MN = AM + BN
c) Chứng minh AM.BN = R^2 (R là bán kính của đường tròn O)
Cho nửa đường tròn tâm O đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi M là điểm bất kì thuộc tia Ax. Qua M kẻ tiếp tuyến với nửa đường tròn, cắt By ở N. Tính số đo góc MON
Cho nửa đường tròn tâm O đường kính AB. Gọi Ax, By là các tia vuông góc với AB Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB . Gọi M là điểm bất kì thuộc tia Ax. Qua M kẻ tiếp tuyến với nửa đường tròn, cắt By ở N. ( E là tiếp điểm)
a)tính góc MON
b) CMR: MN=AM+BN
c)CMR : AM.BN=R^2
d) gọi I là giao điểm của AM và BN, K là giao điểm của EI và AB .CMR: EI vuông góc với AB
cho nửa đường tròn tâm O đường kính AB. gọi Ax, Bx là tia vuông góc với AB(Ax, By và nửa đường tròn thuộc cùng một phẳng bờ AB) gọi M là điểm bất kỳ thuộc tia Ax, qua M kẻ tiếp tuyến với nửa đường tròn, cắt By ở N
a) tính số đo góc MON
b) chứng minh rằng MN=AM+BN
c) chứng minh rằng AM.BN=R2 (R à bán kính của nửa đường tròn)
cho nửa đường tròn tâm O đường kính AB. gọi Ax, Bx là tia vuông góc với AB(Ax, By và nửa đường tròn thuộc cùng một phẳng bờ AB) gọi M là điểm bất kỳ thuộc tia Ax, qua M kẻ tiếp tuyến với nửa đường tròn, cắt By ở N
a) tính số đo góc MON
b) chứng minh rằng MN=AM+BN
c) chứng minh rằng AM.BN=R2 (R à bán kính của nửa đường tròn)
Cho nửa đường tròn tâm O đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi C là 1 điểm bất kì trên nửa đường tròn ( C khác A,B ). qua C kẻ tiếp tuyến với nửa đường tròn cắt Ax, By tại M,N a. Tính MON b. Chứng minh rằng MN = AM + BN c. Chứng minh rằng AM.BN = R2
Cho nửa đường tròn tâm O có đường kính AB (đường kính của một đường tròn chia đường tròn đó thành hai nửa đường tròn). Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn nó cắt Ax và By theo thứ tự ở C và D. Chứng minh rằng:
∠COD = 90o
Cho nửa đường tròn tâm O có đường kính AB (đường kính của một đường tròn chia đường tròn đó thành hai nửa đường tròn). Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn nó cắt Ax và By theo thứ tự ở C và D. Chứng minh rằng:
CD = AC + BD