cho x,y là 2 số thực thỏa x + y=1 . tìm GTNN của A = x3+ y3 + xy + 1
Những câu hỏi liên quan
Cho các số thực dương x, y, z thỏa mãn x3 + y3 + z3 = 24. Tìm GTNN của biểu thức
\(M=\dfrac{xyz+2\left(x+y+z\right)^2}{xy+yz+zx}-\dfrac{8}{xy+yz+zx+1}\)
Cho x , y là các số thực thỏa mãn điều kiện:
3
x
2
+
y
2
-
2
.
log
2
x
-
y...
Đọc tiếp
Cho x , y là các số thực thỏa mãn điều kiện: 3 x 2 + y 2 - 2 . log 2 x - y = 1 2 [ 1 + log 2 ( 1 - x y ) ] . Tìm giá trị lớn nhất của biểu thức M = 2 ( x 3 + y 3 ) - 3 x y .
A. 3
B. 7
C. 17 2
D. 13 2
Cho x,y là các số thực thuộc (0;1) thỏa mãn (x3+y3)(x+y)xy (1−x)(1−y).Tìm giá trị lớn nhất của biểu thức P1√1+x2 +1√1+y2 +4xy−x2−y2
Đọc tiếp
Cho x,y là các số thực thuộc (0;1) thỏa mãn (x3+y3)(x+y)xy =(1−x)(1−y).Tìm giá trị lớn nhất của biểu thức P=1√1+x2 +1√1+y2 +4xy−x2−y2
Không nhìn thấy bất cứ chữ nào của đề bài cả
Đúng 1
Bình luận (0)
Cho x, y là các số thực thỏa mãn điều kiện
3
x
2
+
y
2
-
2
.
log
2
x
-
y
1
2
1
+
log...
Đọc tiếp
Cho x, y là các số thực thỏa mãn điều kiện 3 x 2 + y 2 - 2 . log 2 x - y = 1 2 1 + log 2 1 - x y . Tìm giá trị lớn nhất của biểu thức M = 2(x3 + y3) – xy.
A. 7
B. 13 2
C. 17 2
D. 3
cho x,y là hai số thực dương thỏa mản x3+y3=xy-\(\dfrac{1}{27}\)
tính giá trị của biểu thức p=\(\left(x+y+\dfrac{1}{3}\right)^3-\dfrac{3}{2}\left(x+y\right)+2021\)
\(x^3+y^3+3xy\left(x+y\right)+\dfrac{1}{27}-3xy\left(x+y\right)-xy=0\)
\(\Leftrightarrow\left(x+y\right)^3+\dfrac{1}{27}-3xy\left(x+y+\dfrac{1}{3}\right)=0\)
\(\Leftrightarrow\left(x+y+\dfrac{1}{3}\right)\left[\left(x+y\right)^2-\dfrac{1}{3}\left(x+y\right)+\dfrac{1}{9}\right]-3xy\left(x+y+\dfrac{1}{3}\right)=0\)
\(\Leftrightarrow x^2+y^2-xy-\dfrac{1}{3}\left(x+y\right)+\dfrac{1}{9}=0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(x-\dfrac{1}{3}\right)^2+\left(y-\dfrac{1}{3}\right)^2=0\)
\(\Leftrightarrow x=y=\dfrac{1}{3}\Rightarrow P=...\)
Đúng 2
Bình luận (0)
Cho x+y =1. Tìm GTNN của biểu thức sau : x3+y3+xy
Lời giải:
Theo hằng đẳng thức đáng nhớ thì:
$x^3+y^3+xy=(x+y)(x^2-xy+y^2)+xy=x^2-xy+y^2+xy$
$=x^2+y^2=\frac{1}{2}[(x+y)^2+(x-y)^2]\geq \frac{1}{2}(x+y)^2=\frac{1}{2}$
Vậy GTNN của biểu thức là $\frac{1}{2}$. Giá trị này đạt tại $x+y=1$ và $x-y=0$
$\Leftrightarrow x=y=\frac{1}{2}$
Đúng 0
Bình luận (0)
1.Cho các số thực x, y thỏa mãn x+y+4=0. Tìm GTLN của biểu thức: A= 2(x3+y3)+3(x2+y2)+10xy
Cho hai số thực x,y thỏa mãn:
9
x
3
+
(
2
-
y
3
x
y
-
5
)
x
+
3
x
y
-...
Đọc tiếp
Cho hai số thực x,y thỏa mãn: 9 x 3 + ( 2 - y 3 x y - 5 ) x + 3 x y - 5 = 0 . Tìm giá trị nhỏ nhất của P = x 3 + y 3 + 6 x y + 3 ( 3 x 2 + 1 ) ( x + y - 2 )
Cho 2 số thực x;y thỏa mãn
x
,
y
≥
1
và
log
3
x
+
1
y
+
1
y
+
1
9...
Đọc tiếp
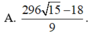
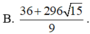
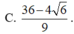
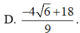
Cho 2 số thực x;y thỏa mãn x , y ≥ 1 và log 3 x + 1 y + 1 y + 1 = 9 − x − 1 y + 1 Biết giá trị nhỏ nhất của biểu thức P = x 3 + y 3 − 57 x + y là một số thực có dạng a + b 7 , a , b ∈ ℤ . Tính giá trị của a+b
A. -28
B. -29
C. -30
D. -31
áp án B
Ta có: log 3 x + 1 y + 1 y + 1 = 9 − x − 1 y + 1 ⇔ y + 1 log 3 x + 1 y + 1 + x − 1 y + 1 = 9
⇔ y + 1 log 3 c + 1 y + 1 + x + 1 y + 1 − 2 y = 11
⇔ y + 1 log 3 c + 1 y + 1 − 2 = 9 − x + 1 y + 1 *
Nếu x + 1 y + 1 > 9 ⇒ V T * > 0 ; V P * < 0
Ngược lại nếu x + 1 y + 1 < 9 ⇒ V T * < 0 ; V P * > 0
Do đó * ⇔ x + 1 y + 1 = 9 ⇔ x y + x + y = 8
Khi đó P = x + y 3 − 3 x y x + y − 57 x + y = x + y 3 − 3 8 − x − y x + y − 57 x + y
Đặt t = x + y ≥ 2 ⇒ f t = t 3 − 3 8 − t t − 57 t = t 3 + 3 t 2 − 81 t
⇒ f ' t = 3 t 2 + 6 t − 81 = 0 ⇒ t = − 1 + 2 7 ⇒ P min = f − 1 + 2 7 = 83 − 112 7 ⇒ a + b = − 29
Đúng 0
Bình luận (0)