\(\ge hi\ lô\le\)

Những câu hỏi liên quan
viết chương trình thực hiện các nhiệm vụ sau đây:
a)Nhập vào từ bàn phím điểm trung bình của n học sinh trong một lớp (1≤n≤100)
b)In ra màn hình số lượng và tỉ lệ học sinh đạt điểm trung bình trở lên(điểm trung bình≥5,0)
uses crt;
var i,d,n:byte;
a:array[1..10]of real;
begin
write('nhap si so lop :');readln(n);
d:=0;
for i:=1 to n do begin
write('nhap diem tb ban thu ',i,' );readln(a[i]);
if a[i]>5.0 then d:=d+1;
end;
writeln('so luong hs dat diem tb tro len la:',d);
writeln('ti le hs dat diem tb tro len la :', (d/n)*100);
readln
end.
Đúng 0
Bình luận (0)
uses crt;
var i,n,d:longint;
a:array[1..100] of real;
d1:real;
begin
clrscr;
write('Nhap so hoc sinh trong mot lop: '); readln(n);
for i:=1 to n do
begin
write('Diem trung binh cua hoc sinh thu ',i,' la: ');readln(a[i]);
end;
for i:=1 to n do
if a[i]>=5 then inc(d);
writeln('So luong hoc sinh dat diem trung binh tro len la: ',d);
d1:=d/n*100;
write('Ti le hoc sinh dat diem trung binh tro len la: ',d1:0:0,'%');
readln
end.
Đúng 0
Bình luận (0)
Miền không bị gạch ở mỗi Hình 12a, 12b là miền nghiệm của hệ bất phương trình nào cho ở dưới đây?a) left{ begin{array}{l}x + y le 2x ge - 3y ge - 1end{array} right.b) left{ begin{array}{l}y le xx le 0y ge - 3end{array} right.c) left{ begin{array}{l}y ge - x + 1x le 2y le 1end{array} right.
Đọc tiếp
Miền không bị gạch ở mỗi Hình 12a, 12b là miền nghiệm của hệ bất phương trình nào cho ở dưới đây?
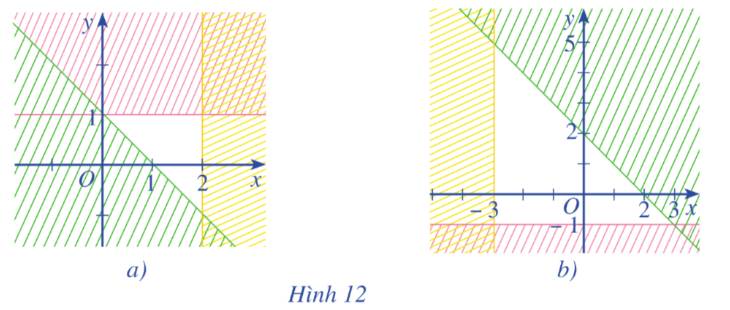
a) \(\left\{ \begin{array}{l}x + y \le 2\\x \ge - 3\\y \ge - 1\end{array} \right.\)
b) \(\left\{ \begin{array}{l}y \le x\\x \le 0\\y \ge - 3\end{array} \right.\)
c) \(\left\{ \begin{array}{l}y \ge - x + 1\\x \le 2\\y \le 1\end{array} \right.\)
Hình 12a
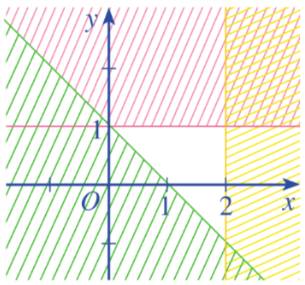
Ta thấy các đường thẳng trên hình là \(y = 1;x = 2;y = - x + 1\)
Từ các phương trình trên thì ta chọn luôn là câu c mà không cần xét tiếp.
Hình 12b.
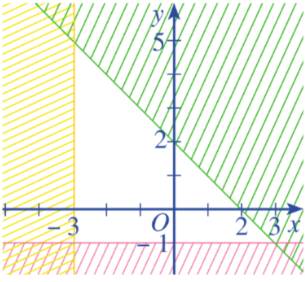
Ta thấy các đường thẳng trên hình là \(y = - 1;x = - 3;x + y = - 2\)
Từ các phương trình trên thì ta chọn luôn là câu a mà không cần xét tiếp
Đúng 0
Bình luận (0)
Biểu diễn miền nghiệm của hệ bất phương trình: \(\left\{ \begin{array}{l}x + y \le 8\\2x + 3y \le 18\\x \ge 0\\y \ge 0\end{array} \right.\)
Tham khảo:
Biểu diễn từng miền nghiệm của mỗi bất phương trình trên mặt phẳng Oxy.
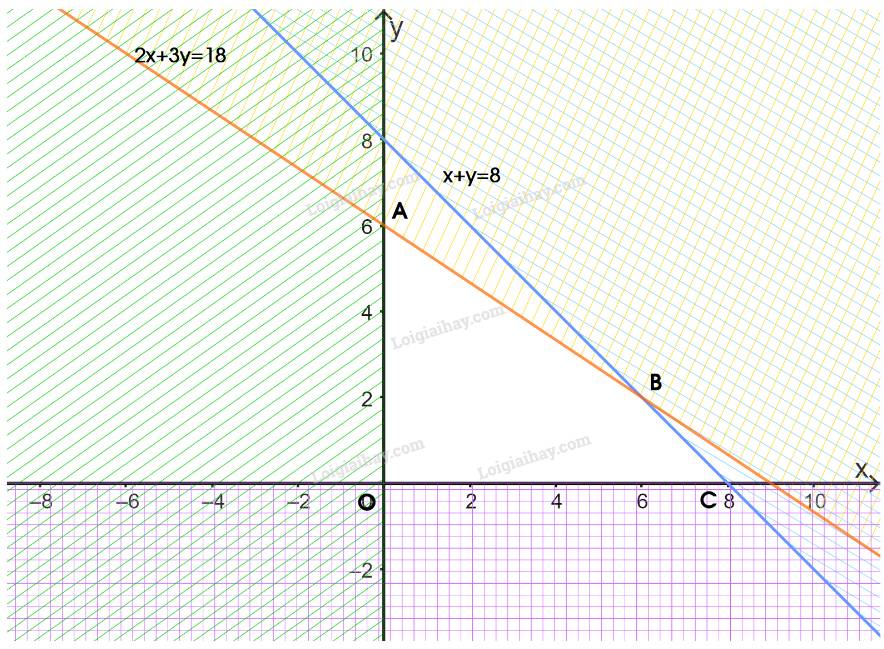
Miền không gạch chéo (miền tứ giác OABC, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình đã cho.
Đúng 0
Bình luận (0)
x-2014ge0 và 2015-xge0 hoặc x-2014le0 và 2015-xle0xge2014 và 2015gex hoặc xle2014 và 2015lex2014lexle2015 hoặc 2015lexle2014(vô lý)Vậy với 2014lexle2015 thì N có giá trị nhỏ nhất là 1
Đọc tiếp
<=>x-2014\(\ge\)0 và 2015-x\(\ge\)0 hoặc x-2014\(\le\)0 và 2015-x\(\le\)0
<=>x\(\ge\)2014 và 2015\(\ge\)x hoặc x\(\le\)2014 và 2015\(\le\)x
<=>2014\(\le\)x\(\le\)2015 hoặc 2015\(\le\)x\(\le\)2014(vô lý)
Vậy với 2014\(\le\)x\(\le\)2015 thì N có giá trị nhỏ nhất là 1
Cho hàm số f(x)=2mx-mx^3.Số x=1là nghiệm của bất phương trình f'(x) ≤1 khi và chỉ khi
A.m≤-1
B.m≥1
C.-1≤m≤1
D.m≥-1
\(f'\left(x\right)=2m-3mx^2\)
\(f'\left(x\right)\le1\Rightarrow2m-3mx^2\le1\Leftrightarrow3mx^2\ge2m-1\)
- Với \(x=1\Rightarrow3m\ge2m-1\Rightarrow m\ge-1\)
Đúng 0
Bình luận (0)
Cho hàm số f(x)=2mx-mx^3.Số=1là nghiệm của bất phương trình f'(x)≤1khi và chỉ khi
A.m≤-1
B.m≥1
C.-1≤m≤1
D.m≥1
Giải chi tiết hộ mình.
hi lô
Cho A =[m;m+2], B=[-1;0]. Khi đó A giao B ≠∅ khi và chỉ khi: ( cho em hỏi là chọn câu nào với lại giải thích giúp em với ạ )
A.m≥ -1 B. m≥-3 C. 0≤m≤ -1 D. -3≤m≤0
Để A⊂BA⊂B thì −1≤m<m+2≤2⇔{m≥−1m≤0⇔−1≤m≤0−1≤m<m+2≤2⇔{m≥−1m≤0⇔−1≤m≤0.
Đúng 0
Bình luận (0)
1, Cho hai tập hợp: A=[2m-1;+∞) ; B=(-∞;m+3] . A giao B ≠ ∅ khi và chỉ khi
A.m≤4 B.m≥3 C.m≥-4 D.m≥4
2. Cho hai tập hợp: A=[m;m+2] ;B=[2m-1;2m+3] . A giao B ≠ ∅ khi và chỉ khi
A. -3<m<3 B.-3<m≤3 C.-3≤m<3 D.-3≤m≤3
( Các bạn giải ra cụ thể giúp mình vs)

















