Chứng minh bất đẳng thức : A = 31x ^4 -6x + 17 > 0

Những câu hỏi liên quan
Chứng minh rằng A=31x4-6x+17>0 với mọi x
Chứng minh đẳng thức, bất đẳng thức: \(9x^2-6x+2>0\) với mọi x
Lời giải:
Ta thấy:
$9x^2-6x+2=(9x^2-6x+1)+1$
$=[(3x)^2-2.3x+1^2]+1=(3x-1)^2+1$
Vì $(3x-1)^2\geq 0$ với mọi $x$
$\Rightarrow 9x^2-6x+2=(3x-1)^2+1\geq 1>0$ với mọi $x$
Ta có đpcm.
Đúng 0
Bình luận (0)
Chứng minh bất đẳng thức sau: 6x4 - 18x3 + 23x2 - 13x + 4 > 0
Bài này đơn giản thôi.
Đặt f(x) = 6x4 - 18x3 + 23x2 - 13x + 4 > 0
\(f\left(x\right)=\frac{47}{54}+\frac{1}{54}\left(18x^2-27x+13\right)^2+\frac{5}{6}x^2\)
Thao tác trên Maple (vào thống kê hỏi đáp xem ảnh)

Còn cách phân tích bằng tay thì qua VMF có bài viết của mình nói về điều này nhé.
chứng minh bất đẳng thức sau
x2 + 6x +9 > 0
x2 + 6x + 10 > 1
a.x2+6x+9>0
(x+3)2>0
Vậy đẳng thức trên đúng
b. x2+6x+10>1
x2+6x+9+1>1
(x+3)2>0
Vậy đẳng thúc trên đúng
Đúng 0
Bình luận (0)
a)\(x^2+6x+9\)
\(\Rightarrow\left(x^2+2.2x.3+3^2\right)\)
\(\Rightarrow\left(x+3\right)^2>0\)
b)\(x^2+6x+10\)
\(\left(x^2+2.2x.3+3^2\right)+1\)
\(\Rightarrow\left(x+3\right)^2+1>1\left(vì\left(x+3\right)^2>0\right)\)
Đúng 0
Bình luận (0)
Chứng minh các bất đẳng thức
a+1/a>=17/42a^4+1/1+a^2>=3a^2-1a+4/(a-b)(b-1)^2>=3 (mọi a>b>=0)Chứng minh bất đẳng thức: \(x^4-4x+5>0\)
Lời giải:
$x^4-4x+5=(x^4-2x^2+1)+(2x^2-4x+2)+2$
$=(x^2-1)^2+2(x-1)^2+2\geq 2>0$ với mọi $x\in\mathbb{R}$
Ta có đpcm.
Đúng 1
Bình luận (0)
Chứng minh các bất đẳng thức sau: \(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\) (với a, b>0)
Biến đổi tương đương:
\(\Leftrightarrow\dfrac{a+b}{ab}\ge\dfrac{4}{a+b}\)
\(\Leftrightarrow\left(a+b\right)^2\ge4ab\)
\(\Leftrightarrow a^2+b^2+2ab\ge4ab\)
\(\Leftrightarrow a^2+b^2-2ab\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\) (luôn đúng)
Vậy BĐT đã cho đúng
Đúng 3
Bình luận (0)
Chứng minh các đẳng thức sau:
a
)
3
2
6
+
2
2
3
−
4
3
2
6
6
b
)
(
x
6
x
+
2
x
3
+
6
x
)
:
6...
Đọc tiếp
Chứng minh các đẳng thức sau:
a ) 3 2 6 + 2 2 3 − 4 3 2 = 6 6 b ) ( x 6 x + 2 x 3 + 6 x ) : 6 x = 2 1 3 v ó i x > 0
a) Biến đổi vế trái:
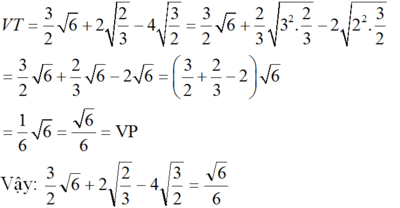
b) Biến đổi vế trái:
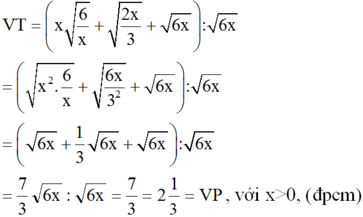
Đúng 0
Bình luận (0)
Chứng minh bất đẳng thức: Với a, b, c >0
tham khảo link: https://lazi.vn/edu/exercise/202136/cho-a-b-c-0-chung-minh-cac-bat-dang-thuc-sau
Đúng 0
Bình luận (0)

















