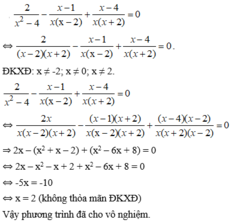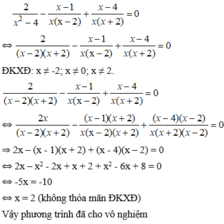\(\left(x+2\right)\left(3-4x\right)=x^2+4x+4\)
\(\Leftrightarrow-4x^2-5x+6=x^2+4x+4\)
\(\Leftrightarrow-5x^2-9x+2=0\)
\(\Leftrightarrow-5x^2-10x+x+2=0\)
\(\Leftrightarrow-5x\left(x+2\right)+\left(x+2\right)=0\)
\(\Leftrightarrow\left(-5x+1\right)\left(x+2\right)=0 \)
\(\Leftrightarrow\left(-5x+1\right)=0\) Hoặc \(x+2=0\)
\(\Leftrightarrow x=\frac{1}{5}\)Hoặc \(x=-2\)
 

(x+2)(3-4x)=x²+4x+4

<=>(x+2)(3-4x)=(x+2)²

<=>(x+2)(3-4x)-(x+2)²=0

<=>(x+2)(3-4x-x-2)=0

<=>(x+2)(1-5x)=0

<=>x+2=0 hoặc 1-5x=0

<=>x=-2 hoặc x=1/5

\(\Leftrightarrow y^2=12-4y\Leftrightarrow z^2=16\Rightarrow z=+-4\Rightarrow\orbr{\begin{cases}y=2\\y=-6\left(loai\right)\end{cases}}\)\(\Rightarrow\left(x-\frac{1}{2}\right)^2=\frac{9}{4}\Rightarrow\orbr{\begin{cases}x=\frac{1}{2}+\frac{3}{2}=2\\x=\frac{1}{2}-\frac{3}{2}=-1\end{cases}}\)

\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)

\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)

\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)

\(\Leftrightarrow x^2-9-x^2+3x=0\)

\(\Leftrightarrow3x-9=0\)

\(\Leftrightarrow3x=9\)

\(\Leftrightarrow x=3\left(n\right)\)

Vậy \(S=\left\{3\right\}\)

\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)

\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)

\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)

\(\Leftrightarrow12x-9-12x+20+2x-7>0\)

\(\Leftrightarrow2x+4>0\)

\(\Leftrightarrow2x>-4\)

\(\Leftrightarrow x>-2\)

2:

a: =>2x^2-4x-2=x^2-x-2

=>x^2-3x=0

=>x=0(loại) hoặc x=3

b: =>(x+1)(x+4)<0

=>-4<x<-1

d: =>x^2-2x-7=-x^2+6x-4

=>2x^2-8x-3=0

=>\(x=\dfrac{4\pm\sqrt{22}}{2}\)

(x + 2)(3 – 4x) =  x 2  + 4x + 4

⇔ (x + 2)(3 – 4x) –  x + 2 2  = 0

⇔ (x + 2)(3 – 4x) – (x + 2)(x + 2) = 0

⇔ (x + 2)[(3 – 4x) – (x + 2)] = 0

⇔ (x + 2)(3 – 4x – x – 2) = 0

⇔ (x + 2)(1 – 5x) = 0 ⇔ x + 2 = 0 hoặc 1 – 5x = 0

      x + 2 = 0 ⇔ x = - 2

      1 – 5x = 0 ⇔ x = 0,2

Vậy phương trình có nghiệm x = - 2 hoặc x = 0,2

\(\Leftrightarrow\left|2x+1\right|=\left|x+6\right|\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+1=x+6\\2x+1=-x-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-\dfrac{7}{3}\end{matrix}\right.\)

ĐKXĐ: \(x\in R\)

\(\sqrt{4x^2+4x+1}=\sqrt{x^2+12x+36}\\ \Leftrightarrow\left|2x+1\right|=\left|x+6\right|\\ \Leftrightarrow\left[{}\begin{matrix}2x+1=x+6\\2x+1=-x-6\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=5\\x=-\dfrac{7}{3}\end{matrix}\right.\)

a/ 4x + 20 = 0

⇔4x = -20

⇔x = -5

Vậy phương trình có tập nghiệm S = {-5}

b/ 2x – 3 = 3(x – 1) + x + 2

⇔ 2x-3 = 3x -3+x+2

⇔2x – 3x = -3+2+3

⇔-2x = 2

⇔x = -1

Vậy phương trình có tập nghiệm S = {-1}
 

câu tiếp theo

a/ (3x – 2)(4x + 5) = 0

3x – 2 = 0 hoặc 4x + 5 = 0

Vậy phương trình có tập nghiệm S= {-5/4,3/2}

b/ 2x(x – 3) – 5(x – 3) = 0

=> (x – 3)(2x -5) = 0

=> x – 3 = 0 hoặc 2x – 5 = 0

* x – 3 = 0 => x = 3

* 2x – 5 = 0 => x = 5/2

Vậy phương trình có tập nghiệm S = {0, 5/2}

b1

a. 4x+ 20=0 <=> 4x= -20 <=> x= -20/4 <=> x= -5

b. 2x- 3= 3(x- 1)+ x+ 2 <=> 2x- 3= 3x- 3+ x+ 2

<=> 2x- 3= 4x- 1 <=> 2x- 4x= -1+ 3 <=> -2x= 2

<=> x= 2/-2 <=> x= -1

b2

a. (3x- 2)(4x+ 5)= 0

<=>\(\orbr{\begin{cases}3x-2=0\\4x+5=0\end{cases}\Leftrightarrow\orbr{\begin{cases}3x=2\\4x=-5\end{cases}}}\)

<=>\(\orbr{\begin{cases}x=\frac{2}{3}\\x=-\frac{5}{4}\end{cases}}\)

b. 2x(x- 3)- 5(x- 3)= 0

<=> (x- 3)(2x- 5)= 0

<=> \(\orbr{\begin{cases}x-3=0\\2x-5=0\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=3\\2x=5\end{cases}}\)

<=> \(\orbr{\begin{cases}x=3\\x=\frac{5}{2}\end{cases}}\)