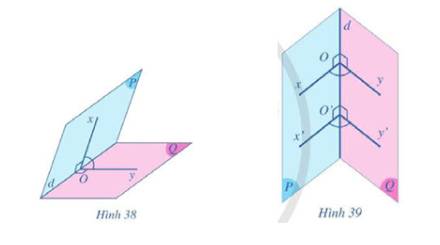
Trong \(\left( P \right)\) ta có:

\(\left. \begin{array}{l}Ox \bot d\\O'x' \bot d\end{array} \right\} \Rightarrow Ox\parallel O'x'\)

Trong \(\left( Q \right)\) ta có:

\(\left. \begin{array}{l}Oy \bot d\\O'y' \bot d\end{array} \right\} \Rightarrow Oy\parallel O'y'\)

Vậy \(\left( {Ox,Oy} \right) = \left( {O'x',O'y'} \right)\) hay số đo của hai góc \(xOy\) và \(x'Oy'\) bằng nhau.

a: góc BEC=1/2*180=90 độ

=>CE vuông góc AB

góc BDC=1/2*180=90 độ

=>BD vuông góc AC

góc AEH=góc ADH=90 độ

=>AEHD nội tiếp

b:

Gọi K là trung điểm của AH

=>K là tâm đường tròn ngoại tiếp tứ giác ADHE

góc KDO=góc KDH+góc ODH

=góc KHD+góc OBD

=90 độ

=>OD là tiếp tuyến của (K)

a) Vì AH, HB, AB đều là các đường kính của các nửa đường tròn (O₁) , (O₂) và (O) nên tứ giác MPHQ có ba góc P, Q, M vuông. Vì vậy nó là hình chữ nhật.

Từ đó, ta có HM = PQ.
b) Vì MHPQ là hình chữ nhật nên \widehat{MPQ}=\widehat{MHQ}=\widehat{MBH}\left(=\dfrac{\stackrel\frown{HQ}}{2}\right)MPQ​=MHQ​=MBH(=2HQ⌢​​), do đó APQB là tứ giác nội tiếp.

c) Ta có \widehat{O_1PA}=\widehat{PAO_1}=90^o-\widehat{HMP}=90^o-\widehat{MPQ}O1​PA​=PAO1​​=90o−HMP=90o−MPQ​

\Rightarrow\widehat{O_1PA}+\widehat{MPQ}=90^o\Rightarrow\widehat{O_1PQ}=90^o⇒O1​PA​+MPQ​=90o⇒O1​PQ​=90o nên PQ tiếp xúc nửa đường tròn (O₁) tại P. 

Tương tự , PQ tiếp xúc (O₂) tại Q hay PQ là tiếp tuyến chung của hai nửa đường tròn (O₁) và (O₂)

a,Xét (O1) có góc APH nội tiếp chắn nửa đtròn

⇒ góc APH = 90

Mà góc APH + góc MPH = 190( 2 góc kề bù)

⇒ góc MPH = 90 (1)

Xét (O2) có góc HQB nội tiếp chắn nửa đtròn

⇒ góc HQB = 90

Mà góc HQB + gócHQM   = 190( 2 góc kề bù)

⇒ góc HQM = 90 (2)

Xét (O) có góc AMB nội tiếp chắn nửa đtròn

⇒ góc AMB = 90 hay góc PMQ = 90 (3)

Từ 1 2 3 ⇒ tg PMQH là hcn ( tg có 3 góc vuông)

⇒MH = PQ

b, Xét tg APQB 

Có góc APH =90 (cmt)

      góc HQB =90(cmt)

 ⇒ góc APH = góc HQB = 90

Nên tg APQB nt ( tg có 2 định P và Q kề nhau cùng nhìn cạnh AB dưới những góc bằng nhau bằng 90)

c, Ta có: góc O1PA = góc PAO1

                               = 90 - góc HMP

                               = 90 - góc MPQ

⇒ góc O1PA +góc MPQ=90

⇒ O1PQ = 90

⇒ PQ⊥ PO1

    P tx với nửa đtròn tại p

⇒PQ là tiếp tuyến (O1)

CM tương tự có PQ là tt (O2)

⇒ PQ là tt chung của 2 đtròn O1 và O2

a) 
► Tính chất của hai tiếp tuyến cùng xuất phát từ một điểm, ta có: 
AC = CM ; BD = MD 
=> AC + BD = CM + MD = CD 
► Câu trên có thể cm trực tiếp bằng cách nối OC => hai tgiác ACO và MCO bằng nhau (vì tgiác vuông, có chung cạnh huyền, OA=OM=R) 
=> OC là tia phân giác của góc AO^M 
tương tự: OD cúng là phân giác cua góc BO^M 
AO^C + CO^M + DO^M + DO^B = 180o 
=> 2.CO^M + 2DO^M = 180o 
=> CO^M + DO^M = CO^D = 90o 
► tgiác COD vuông có OM là đường cao, hệ thức lượng: 
CM.MD = OM² 
=> AC.BD = R² (cm trên: AC=CM; BD=MD; OM=R) 
► ad toilet với chú ý AC//BD 
NC/NB = AC/BD = CM/MD 
định lí đảo talet => MN//AC 
► có: MN//AC//BD => hai tgiác CBD và CNM đồng dạng 
=> CD/CM = DB/MN 
=> CD.MN = CM.DB 
► gọi K là trung điểm CD 
do tgiác OCD vuông tại O => K là tâm đường tròn ngoại tiếp tgíc OCD 
OK là đường trung bình của hình thang ABDC => OK//AC//BD 
=> OK vuông góc AB tại O 
=> AB là tiếp tuyến của đường tròn (OCD) 

b) 
► ta đã cm: AC+BD = CD 
=> AC+BD nhỏ nhất khi CD nhỏ nhất 
Có Ax //By, C thuộc Ax, D thuộc By 
=> CD nhỏ nhất khi CD vuông góc vơi Ax và By 
khi đó ta có ABDC là hình chữ nhật 
=> M là điểm chính giữa của cung AB 
► tứ giác ABDC thường là hình thang vuông, gọi diện tích là S 
S = (1/2)AB.(AC+BD) = (1/2).AB.CD 
vì AB cố định nên S nhỏ nhất khi CD nhỏ nhất 
như câu trên có M là điểm chính giữa cung AB 

c) tgiac OAM cân tại O, lại có OE là phân giác => OE vuông AM 
tương tự OF vuông BM, mà CO^D= 90o 
=> EOFM là hình chữ nhật 
=> I là trung điểm EF cũng là trung điểm OM 
=> OI = OM/2 = R/2 
I di động nhưng luôn có OI = R/2 không đổi 
=> I thuộc đường tròn cố định: tâm O bán kính r = R/2 
** giới hạn: M chỉ di động trên nữa đường tròn (O,R) => I chỉ di động trên nữa đường tròn (O,r) nằm cùng phía với (O,R) so với AB 
<< phần giới hạn là khuyến mãi thêm, vì đề chỉ yêu cầu cm I thuộc một đường tròn cố định, không phải tìm quỉ tích >> 

d) dùng định lí Melanus là nhanh nhất: có ngay E,N,F thẳng hàng => EF/AB = ME.MA = MN/MJ = 1/2 
=> MN = MJ/2 = NJ 

Em tham khảo tại link dưới đây nhé.

Câu hỏi của My Trấn - Toán lớp 9 - Học toán với OnlineMath

Câu c) Đã có IK // AD thì ta vận dụng Ta let và thấy ngay : 

\(\frac{IC}{AD}=\frac{IK}{AD}\Rightarrow IC=IK\)